Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 03. 2016 19:59
Vlasnost grupy
Pozdravujem.
Nech x, y su dva prvky jednej grupy G ( konecna alebo nie). Dokazte ze rad xy je rovny radu yx.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 18. 03. 2016 23:43
Re: Vlasnost grupy
Offline
#3 19. 03. 2016 02:09
Re: Vlasnost grupy
Ahoj ↑ holyduke:,
Dobre myslienky, ale chybaju upresnenia tykajuce sa k, p.
Presnejsie:
Tvoja relacia  neznamena este, ze
neznamena este, ze  je rad prvku xy.
je rad prvku xy.
Ako treba upresnit tvoj pokus dokazu, aby sa stal skutocny dokaz?
Poznamka: tvoje oznacenie grupy multiplikativnym sposobom je dobre vybrane ( podla zvyku oznacenia nekomutativnych grup, a vtedy sa moze pisat 1, miesto e).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 19. 03. 2016 10:16 — Editoval vanok (19. 03. 2016 10:38)
Re: Vlasnost grupy
↑ holyduke:,
Ano,
A tak napr. Nech p, k su respektivne rady prvkov xy a yx
Tvoja prva skupina implikacii rovnosti z komentarmy 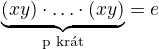 ( kompozicia na lavo prvkom
( kompozicia na lavo prvkom  a na pravo prvkom
a na pravo prvkom  , da po pouziti associativityp)
, da po pouziti associativityp)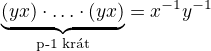 (...)
(...)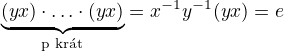
Posledna rovnosti, z nich da, ze rad k prvku yx deli rad p prvku xy.
A podobne opacna implikacia....
Na koniec je lahko vidiet, tento dokaz plati aj pre nekonecne grupy.
(
Cize klucova myslienka je, ze napr. 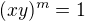 , m kladne, znamena ze rad p prvku xy deli m.
, m kladne, znamena ze rad p prvku xy deli m.
Tak oprav a dopln tvoj pokus dokazu, aby to dalo dokonaly dokaz.
Poznamka: pridam, tu na fore, dalsie cvicenia z teorie grup, pre ktore sa casto vidia nedostatocne riesenia ...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 25. 03. 2016 12:59
Re: Vlasnost grupy
↑ vanok:
Tak teda dokonaleji:
Mějme grupu 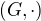 s neutrálním prvkem
s neutrálním prvkem  .
.
Dokazujeme, že  kde
kde  (resp.
(resp.  ) je řád prvku
) je řád prvku 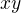 (resp.
(resp. 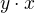 )
)
Podle prvního vztahu platí:
Jelikož se pohybujeme v grupě, můžeme využít asociativitu a libovolně přezávorkovat:
Jelikož ke každému prvku určitě existují inverzní prvky, můžeme vynásobit rovnici 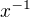 zleva a
zleva a  zprava, na pravé straně využijeme vlastnosti neutrálního prvku:
zprava, na pravé straně využijeme vlastnosti neutrálního prvku:
Využijeme vlastnosti inverzních prvků: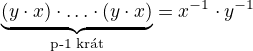
Vynásobíme prvkem 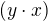 zprava a opět s využitím inverzních prvků a asociativity máme:
zprava a opět s využitím inverzních prvků a asociativity máme:
Takže: 
Tím p musí být nutně násobkem k, neboli 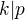 .
.
Analogicky bychom ukázali, že také 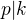 .
.
Dostáváme tedy 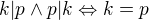 .
.
Offline

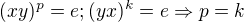


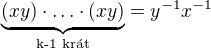
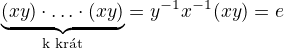
 a celkově
a celkově 