Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Vzdialenosti na strednej skole
#1 02. 03. 2016 17:15
Vzdialenosti na strednej skole
Pozdravujem
V cviceniach ako tu, 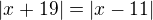 sa casto zabuda na geometricko- topologicku interpretaciu: rovnica znamena, ze d(x,-19)=d(x,11) d= distance= vzdialenost
sa casto zabuda na geometricko- topologicku interpretaciu: rovnica znamena, ze d(x,-19)=d(x,11) d= distance= vzdialenost
Cize x je rovnako vzdialeny od -19 a 11.
Takuto uvahu, ako tuto co napisal vyssie som na stredoskolskom fore este nevidel.
Nie je to skoda?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 09. 03. 2016 08:59
Re: Vzdialenosti na strednej skole
Pozdravujem,
Nikto sa z takovto situaciou nestretol?
A vseobecnejsie ine "vzdialenosti " by nezaujali stredoskolakov?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 09. 03. 2016 09:36
Re: Vzdialenosti na strednej skole
↑ vanok:
Zdravím.
Nevím jak to vypadá ve Francii (a vlastně v současnosti ani v ČR) na středních školách, ale když jsem navštěvoval gymnázium já, tak touto úvahou jsme celé téma začínali.
Takže my jsme na tuto interpretaci nezapomínali.
Problém je, že při řešení komplikovanějších příkladů už tento přístup moc nepomůže.
A další věc (ale je to jen můj názor): Studenti se učí řešení rcí s a.h. proto, aby zvládli METODU. Tyto rovnice totiž nemají v podstatě mimo školu žádné praktické využití.
Ale metoda "složitý problé rozděl na jednodušší, ty vyřeš, a pak udělej syntézu řešení" je univerzální a velmi užitečná téměř všude.
Pak je ale lepší nutit studenty používat tento přístup, i když by určitý konkrétní příklad šel vyřešit i jinak a rychleji.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 09. 03. 2016 11:43 — Editoval vanok (09. 03. 2016 11:43)
Re: Vzdialenosti na strednej skole
Pozdravujem ↑ zdenek1:,
Dakujem za tvoj zaujem o tuto temu.
Nutit deti nieco robit, to urcite nie ( ak niekto nechce, tak sme bezmocni). Ale ukazat, to moze byt uzitocne a ze je to ucinne to ano. A mozno to vytvori ludi co budu vedecka elita.
Vo Fr neviem co sa robi na takej urovni. Ale vyucujuci su velmi viazani osnovami.
Mozno v CR maju viac slobody.
Ale ked sa pozreme na cvicenia dane na roznych olympiadach, take neskolske uvahy sa pacia....
Mozno dnes uz nie je vela moznosti v skole detom ukazat nieco ine ako "skolske" metody, tie ine su skor pre matematicke kruzky, kde sa da naucit nieco co vedie k mysleniu.
Co sa tyka inych vzdialenosti, myslel som napriklad na https://en.m.wikipedia.org/wiki/Taxicab_geometry .
To su mozno temy, ktore by mohli byt velmi uzitocne, aspon na temu "matematika to je mysliet ", a mohli by doplnit prace kolegov fyzikov co chcu ukazat fyziku s luckou tvarou.( dufam pre nich ze sa im podari urobit ich knihu)
Mozno by bolo zaujimave v tomto vlakne diskutovat aspon o vzdialenostiach co mozu byt uzitocne pre stredoskolakov co sa zaujimaju o matematiku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 12. 03. 2016 12:19
- check_drummer

- Příspěvky: 4939
- Reputace: 106
Re: Vzdialenosti na strednej skole
↑ vanok:
Ahoj, středoškoláky by např. mohla zajímat vzdálenost od učebny A k východu Z ze školy. Kromě poněkud humorného náboje, by na tomto tématu mohli seriozně zkoumat pojem vzdálenosti. trochu to připomíná manhattanskou metriku - tady by to bylo dokonce ve třech rozměrech (má-li škola více pater).
"Máte úhel beta." "No to nemám."
Offline
#6 12. 03. 2016 12:43
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Vzdialenosti na strednej skole
↑ check_drummer:Vtipne :)
Prezouva se na strednich skolach? Protoze potom bysme prisli o manhattanskou metriku a meli bych spise neco jako washingtonskou a zajimavy pripad neekvivalentnich metrik (Pokud je ucebna blizko vychodu, nijak to nepomuze studentum kteri se chodi prezouvat so satny.)
PS: Normalne je teda asi satna nekde u vchodu, ale my jsme se chodili okolo vchodu prezouvat kamsi do sklepa a potom stejnou cestou zpet :).
Offline
#7 30. 03. 2016 16:10
Re: Vzdialenosti na strednej skole
↑ kaja.marik:↑ check_drummer:,
Zaujimave poznamky.
A nech zije matematika, ked sa musi mysliet a mozu sa zabudnut recepty.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Vzdialenosti na strednej skole
