Matematické Fórum

Feek · 31. 03. 2016 17:27

//forum.matweb.cz/upload3/img/2016-03/35399_int.jpg

Poradí prosím někdo, jak na tento integrál? Je mi jasné, že je třeba použít Fubiniho větu přes množinu jednoho ze dvou typů, ale jak zvolit správné meze integrace?

Napadají mne dvě varianty (každá vychází jinak):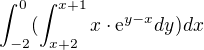

$\int_{-2}^{0}(\int_{x+2}^{x+1}x\cdot \mathrm{e}^{y-x}dy)dx$

$\int_{0}^{2}(\int_{y-1}^{y-2}x\cdot \mathrm{e}^{y-x}dx)dy$

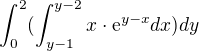
Je jedna z nich správná, nebo je to úplně jinak?

Jj · 31. 03. 2016 18:34

↑ Feek:

Dobrý den.

Řekl bych, že poněkud jinak. Nákres množiny M není v úloze samoúčelně: Odkaz.

Meze (jednu z variant) bych pak viděl takto:

$\int_{-2}^{-1}\int_{0}^{x+2}f(x,y)\, dy\,dx \quad + \quad \int_{-1}^{0}\int_{x+1}^{x+2}f(x,y)\, dy\,dx$

Feek · 01. 04. 2016 09:52

↑ Jj:

Ano, již vidím v čem je problém. Mé dva návrhy integrují vždy přes poněkud větší množinu, než je ta ze zadání.

Děkuji za pomoc!

Matematické Fórum

#1 31. 03. 2016 17:27

Dvojný integrál přes množinu

#2 31. 03. 2016 18:34

Re: Dvojný integrál přes množinu

#3 01. 04. 2016 09:52

Re: Dvojný integrál přes množinu

Zápatí