Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2016 11:36
rozklad na parcialne zlomky
ahojte, mam rozlozit na parcialne zlomky vyraz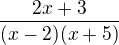 postupoval som
postupoval som  z toho som dostal rovnicu
z toho som dostal rovnicu 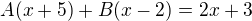 z toho som vytvoril
z toho som vytvoril 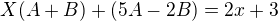 odtial som dostal dve rovnice
odtial som dostal dve rovnice  a
a 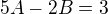 a odtial
a odtial  ,
, 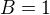 mam to spravne? podla mna asi nie lebo po dosadeni mi vychadza
mam to spravne? podla mna asi nie lebo po dosadeni mi vychadza  a to sa nerovna povodnemu vyrazu
a to sa nerovna povodnemu vyrazu 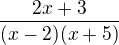
Offline
- (téma jako vyřešené označil(a) Statistik)
#8 16. 04. 2016 22:05
- misaH
- Příspěvky: 13439
Re: rozklad na parcialne zlomky
↑ Statistik:
Google: zakrývacia metóda
http://math.feld.cvut.cz/mt/txtd/3/txc3db3i.htm
Offline
#9 16. 04. 2016 22:06 — Editoval Kenniicek (16. 04. 2016 22:07)
Re: rozklad na parcialne zlomky
Vychadzam z tohto (pravu stranu vo vypocte ani nepouzivam, je tam len na zapametanie, ktore pismeno pocitam): 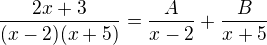
Na lavej strane si zakryjem/odmyslim (x-2) a dosadim tento koren, cize 2, do zvysneho zlomku: 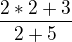
Z tohto mam hned, ze A = 1
Takisto to bude fungovat v priapade Bcka.
Offline
#10 16. 04. 2016 22:21
- misaH
- Příspěvky: 13439
Re: rozklad na parcialne zlomky
↑ Kenniicek:
Že sa ti to chce... ako keby si zadávateľ nemohol na svoju otázku odpovedať cez Google sám.
Dávaj udicu, nie rybu. Alebo ti ide o niečo iné ako o pomoc?
Offline