Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Binomický koeficient (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 04. 2016 13:58 — Editoval Marian (21. 04. 2016 14:00)
Binomický koeficient
Ač patrně spíše standardní a jednoduché, jistě bude mít mnoho studentů z řad SŠ problém dokázat, že platí
Dokažte.
PS: Věřím, že nikdo nebude zatěžovat potenciální řešitele odkazy z internetu, které se spíše hodí jako doplnění již uvedených pokusů řešení.
Offline
- (téma jako vyřešené označil(a) Marian)
#2 21. 04. 2016 15:08
Re: Binomický koeficient
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 21. 04. 2016 21:33
Re: Binomický koeficient
Pozdravujem ↑ Marian:,
Som myslel, ze cakas riesenie od skutocnych stredoskolakov.
Teraz ked to najznamejsie riesenie je uz napisane, nemohol by si napisat nieco viac o Catalan-ovych cislach. Vsak ide o velmi peknu matematicku historiu.
Prijemny vecer.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 22. 04. 2016 18:22
Re: Binomický koeficient
↑ vanok:
Taktéž pozdravuji. I já jsem očekával spíše řešení středoškoláka, ale Pavel snědl tento matematický zákusek s velkou chutí (případně se středoškoláci přiučí, případně najdou jiný přístup k řešení problému).
Historie Catalanových čísel může být jistě hezká story, ale necítím se k tomu povolán. Pokud máš nějaký hezký odkaz, jistě se v tuto chvíli hodí a vhodně doplní to, co se v řešení nevyskytlo, nebo z povahy věci ani nemohlo vyskytnout.
Offline
#7 24. 04. 2016 15:39
Re: Binomický koeficient
↑ Jenda358:
Nemám to rozmyšlené, ale řekl bych, že půjde vylepšit kombinatorický důkaz Bertrandova postulátu, až budu mít čas, zkusím se na to podívat.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 24. 04. 2016 17:11
#9 25. 04. 2016 19:10
Re: Binomický koeficient
Pozdravujem ↑ Marian:,
Zatial nemam vela casu, ale ked najdem nieco zaujimave to sem dam.
Zatial aspon toto youtube https://www.youtube.com/watch?v=z_75zzqXVnM
Aj druha cast je zaujimava.
Pekny vecer.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Binomický koeficient (TOTO TÉMA JE VYŘEŠENÉ)


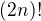 dělitelné číslem
dělitelné číslem  .
. platí
platí
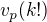 a faktu, že pre
a faktu, že pre 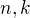 prirodzené a
prirodzené a  je
je