Matematické Fórum

Janisek · 26. 04. 2016 17:36

Zdravím, při přípravě k maturitě jsem narazil na tento příklad.. Vím, že to budu řešit substituční metodou a že budu nahrazovat 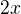$2x$ třeba za $t$ . Pak tuto substituci zderivuju a dosadím za 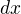$dx$ $dx=\frac{1}{2}dt$ Dál už to bohužel nejsem schopný dopočítat.. Přitom výsledek je tak jednoduchý.. Díky za cenné rady..
Příklad:
$\int_{}^{}\frac{cos^{2}2x}{1+sin2x}dx$

Jj · 26. 04. 2016 17:50

↑ Janisek:

Dobrý den.

Řekl bych, že je vhodné integrand nejdříve upravit:

$\int\frac{cos^{2}2x}{1+sin2x}\,dx=\int\frac{1-sin^{2}2x}{1+sin2x}\,dx=\int\frac{(1+sin 2x)(1-sin 2x)}{1+sin2x}\,dx=\cdots$

Takže zkrátit a pak integrovat.

Al1 · 26. 04. 2016 17:52 — Editoval Al1 (26. 04. 2016 17:53)

↑ Janisek:

Zdravím,

a nechceš nejprve integrand upravit?
$\int_{}^{}\frac{\cos^{2}2x}{1+\sin 2x}dx=\int_{}^{}1-\sin(2x) dx$

A pak teprve zavést substituci, pokud dokonce neupravíš zpaměti.

Jinak v tvém případě $\int_{}^{}\frac{\cos^{2}2x}{1+\sin2x}dx=\frac{1}{2}\int_{}^{}\frac{cos^{2}t}{1+sin t}dt$ a teď bych zase zkusil nejprve upravovat inetgrand

Edit: kolega Jj (zdravím) byl rychlejší, ale ponechám.

Matematické Fórum

#1 26. 04. 2016 17:36

Integrální počet

#2 26. 04. 2016 17:50

Re: Integrální počet

#3 26. 04. 2016 17:52 — Editoval Al1 (26. 04. 2016 17:53)

Re: Integrální počet

Zápatí