Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 04. 2016 14:38
- zzllaattkkaa

- Zelenáč
- Příspěvky: 9
- Pozice: student
- Reputace: 0
Plošný obsah elipsoidu
Prosím o pomoc v výpočtem plošného obsahu elipsoidu 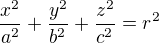 měli bychom to počítat pomocí první základní formy, ale vůbec nevím, co s tím...
měli bychom to počítat pomocí první základní formy, ale vůbec nevím, co s tím...
Offline
#2 02. 05. 2016 09:21 — Editoval Rumburak (02. 05. 2016 10:36)
Re: Plošný obsah elipsoidu
↑ zzllaattkkaa:
Ahoj.
Danou plochu  si rozdělíme na dvě části podle toho, zda je
si rozdělíme na dvě části podle toho, zda je 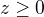 nebo
nebo  , jejichž obsahy
, jejichž obsahy
se neliší (elipsa, která je odděluje, má plošnou míru 0 a proto je lhostejno, ke které z nich ji přidáme).
Počítejme obsah první plochy popsané rovnicí  , kde
, kde
 .
.
Můžeme zde použít vzorec
 ,
,
v němž  je kolmý průmět daného elipsoidu do roviny Pxy.
je kolmý průmět daného elipsoidu do roviny Pxy.
Ale jsou i další možnosti.
Offline