Matematické Fórum

madla26 · 17. 05. 2014 11:25

Dobrý den, vůbec nevím, jak na následující příklad:
Dva světelné paprsky dopadají na rozhraní vzduchu a kapaliny tak, že jsou navzájem kolmé. Určte index lomu kapaliny, jestliže úhel lomu jednoho paprsku je 36 stupňů a druhého 20 stupňů.

Moc děkuji za pomoc.

runcorne · 17. 05. 2014 11:37

↑ madla26:
Index lomu daného prostředí se nemění, takže musí platit, že:
$\frac{\sin \alpha _{1}}{\sin \beta _{1}}=\frac{\sin \text{ }(90^\circ -\alpha _{1})}{\sin \beta _{2}}$
Úpravou získáme:
$\text{tg}\text{ }\alpha _{1}=\frac{\sin \beta _{1}}{\sin \beta _{2}}$
Z toho je
$\alpha _{1} = 59,81^\circ$
A stačí dopočítat n:
$n=\frac{\sin \alpha _{1}}{\sin \beta _{1}}\doteq 1,5$

kostra · 28. 05. 2014 18:08

Dobrý den chtěl bych Vás poprosit o pomoc s příkladem: Vypočítej poloho obrazu při zobrazení předmětu dutým zrcadlem s ohniskovou vzdáleností 30cm, je-li předmět ve vzdálenosti 60cm před zrcadlem. Pomocí rovnice pro zvětčení urči jaké budou vlastnosti obrazu. Předem děkuji za pomoc.

darkorbit · 29. 05. 2014 11:20

↑ kostra:

Ahoj

skús použiť zobrazovaciu rovnicu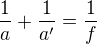
$\frac{1}{a}+\frac{1}{a'}=\frac{1}{f}$
kde " a " je vzdialenosť predmetu od zrkadla a " a' " je vzdialenosť obrazu od zrkadla.
Potom použi rovnicu pre zväčšenie:
$Z=-\frac{a'}{a}$
Konvencia je - záporné zväčšenie znamená prevrátený obraz, jeho abs. hodnota určuje pomer výšky obrazu a predmetu, záporná vzdialenosť " a' " znamená obraz neskutočný.

Tým máš zbrane nabité, môžeš útočiť.

Good luck.

AndrejR · 10. 05. 2016 21:00

runcorne napsal(a):
↑ madla26:
Index lomu daného prostředí se nemění, takže musí platit, že:
$\frac{\sin \alpha _{1}}{\sin \beta _{1}}=\frac{\sin \text{ }(90^\circ -\alpha _{1})}{\sin \beta _{2}}$
Úpravou získáme:
$\text{tg}\text{ }\alpha _{1}=\frac{\sin \beta _{1}}{\sin \beta _{2}}$
Z toho je
$\alpha _{1} = 59,81^\circ$
A stačí dopočítat n:
$n=\frac{\sin \alpha _{1}}{\sin \beta _{1}}\doteq 1,5$

Ahoj, jak je možné, že tam je $90-\alpha$ ? Pokud to platí a alfa vyjde 59,81, pak neplatí kolmost v zadání.

runcorne · 10. 05. 2016 23:09

↑ AndrejR:

Zdravím,

proč neplatí?

$\alpha _{1} = 59,81^\circ$
$\alpha _{2} = 30,18^\circ$

Vztah $90-\alpha_{1}$ vychází z toho, že -- pokud jsou kolmé -- musí platit:

$\alpha _{1} +\alpha _{2} = 90^\circ$