Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2013 12:28
Kuželosečky - kružnice
Zdravím, mohl by mi někdo pomoci vyřešit tento zapeklitý příklad?
Napište rovnici kružnice vepsané trojúhelníku KLM, je-li ![kopírovat do textarea $K[2,1], L[6,4], M[6,1]$](/mathtex/ee/ee5a0aab96a93a9134984bee66c774f6.gif)
Došla jsem k tomu, že poloměr kružnice je jedna a že trojúhelník má pravý úhel u vrcholu M, jen nevím, jak dopočítat souřadnice středu (m,n). Děkuji všem za pomoc.
Výsledek: 
Offline
- (téma jako vyřešené označil(a) mark72)
#2 03. 02. 2013 12:45
Re: Kuželosečky - kružnice
Ahoj ↑ mark72:,
ja by som na výpočet súradníc m, n stredu S použila vzorec pre vzdialenosť bodu od priamky v rovine.
Bod S je od priamky KM vzdialený o jedna, zo vzorca pre vzdialenosť potom vyjde  ,
,
odtiaľ n=0 alebo n=2, a keďže S leží v polrovine KML, je jednoznačne n=2.
Obdobne pre vzdialenosť bodu S od priamky LM.
Vyjde  ,
,
odtiaľ m=5 alebo m=7, a opäť vzhľadom na polroviny m=5.
server.gphmi.sk/~domanyov
Offline
#4 12. 05. 2016 15:22
Re: Kuželosečky - kružnice
↑ thatsmis:
Vzorec pro výpočet poloměru kružnice vepsané trojúhelníku viz Odkaz
Pokud se tedy nemýlím.
Offline
#5 12. 05. 2016 15:45
Re: Kuželosečky - kružnice
↑ Jj:už som celkom domýlená. Vedela som si vpočítať, že trojuholník je pravouhlý s pravým uhlom pri vrchole M. Taktiež som si našla dve osi uhla pri vrchole M, ktoré mi vyšli o1: x-y-5=0 a o2: x+y-7=0. Ďalej som si našla osi uhla pri vrchole K, ktoré mi vyšli o1: x-3y+1=0 a o2: 3x+y-7=0. Spravila som ich prienik, ale bohužial súradnice stredu nevychádzajú tak ako majú. Neviete mi prosím poradiť, ako z tohto ďalej ?
Offline
#6 12. 05. 2016 16:02 — Editoval gadgetka (12. 05. 2016 16:03)
Re: Kuželosečky - kružnice
Ahoj, dalo by se to řešit i přes osu úhlu. Osa úhlu je určena vrcholem a směrovým vektorem.
Osa úhlu je vlastně „průměr směrů obou ramen“, tzn., že určíme jednotkové vektory  ramen (svírající daný úhel) a směrový vektor osy úhlu je pak součtem jednotkových vektorů (
ramen (svírající daný úhel) a směrový vektor osy úhlu je pak součtem jednotkových vektorů ( ).
).














Průsečík os = střed kružnice opsané:

----------------
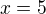
![kopírovat do textarea $S[5; 2]$](/mathtex/3a/3a71f9c68eea11e267704cafff50ef5b.gif)
Poloměr: vzdálenost středu od (např.) strany KM


Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 12. 05. 2016 20:49
Re: Kuželosečky - kružnice
↑ thatsmis:
Jistě, jde to přes osy úhlů, ale pro menší trápení se přimlouvám spočítat poloměr vepsané kružnice přes plochu daného trojúhelníka vyjádřenou jednak pomocí odvěsen, jednak pomocí uvedeného poloměru (což odpovídá vzorečku v odkazu tady ↑ Jj:):
Pokud se tedy nemýlím.
Offline
#8 13. 05. 2016 07:24 — Editoval Cheop (13. 05. 2016 07:24)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Kuželosečky - kružnice
↑ thatsmis:
Všechny 3 osy úhlu mají rovnice:
Z toho střed kružnice 
poloměr je vzdálenost středu od přímky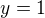 tj.
tj.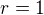
Nikdo není dokonalý
Offline



