Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 05. 2016 19:59 — Editoval Freedy (11. 05. 2016 20:25)
Polynom
Dobrý den,
mám takový dotaz.
Jestliže mám polynom
tak vím, že můžu vytknout x^2. Nicméně o to mi nejde.
Tento polynom má 2-násobný kořen 0 a pak žádný reálný.
Nicméně, existují takové koeficienty,  ,
,  tak, že platí
tak, že platí
Například pokud mám polynom 
tak ten umím rozložit jako 
Ale tak to je triviální. Lze nějak dokázat, že taková čísla existují? popřípadě je najít?
Mám na mysli něco ve smyslu, že lze brát v potaz rozklady podobné například tomuto
nicméně potřebuji mít koeficienty u x buď 1 nebo 0. Exponenty můžou být reálné.
Díky, Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#2 12. 05. 2016 01:05
Re: Polynom
Ahoj ↑ Freedy:. se mi zdá dost nadsazený. Pro záporný exponenty to neplatí a pro kladný se očividně stačí omezit na
se mi zdá dost nadsazený. Pro záporný exponenty to neplatí a pro kladný se očividně stačí omezit na  . Potom tu ale máš tvrzení z algebry, že
. Potom tu ale máš tvrzení z algebry, že ![kopírovat do textarea $\mathbb{Z}[X]$](/mathtex/2f/2fc6489512d083678e4ee785fb78d46d.gif) je UFD (unique factorization domain), z čehož plyne, že tvůj rozklad neexistuje pro každý ireducibilní polynom nad
je UFD (unique factorization domain), z čehož plyne, že tvůj rozklad neexistuje pro každý ireducibilní polynom nad 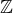 (sporem).
(sporem).
Offline
#3 13. 05. 2016 01:22
Re: Polynom
↑ Bati:
sice toto tvrzení z algebry nemám, jelikož ji ještě nemám, ale budu tomu věřit.
Nicméně, lze nějak ukázat, že taková "reálná" čísla existují nebo ne?
Názor od jednoho docenta:
netroufám si říct, že v reálných číslech to nelze
Sestavil jsem si tabulku, co pro exponenty musí platit, nicméně těch možností je tak moc, že to ručně neprozkoumám. Jak tedy "na to"
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 13. 05. 2016 10:48 — Editoval Bati (13. 05. 2016 10:55)
Re: Polynom
↑ Freedy:
Podle mě jsem ti už odpověděl...
1) Zkoumat ryze reálný exponenty se mi zdá nesmyslný (vzhledem k tomu, že při násobení se sčítají, je jich konečně mnoho a výsledkem musí být celé číslo)
2) Pokud uvažuješ racionální exponenty, tak taková čísla neexistují pro každý ireducibilní polynom, jak jsem ti už napsal.
Jinak ta věta z algebry, kterou jsem zmínil je jen jinak zapsaný fakt, že Euklidův algoritmus funguje i pro polynomy, což se dá snadno ověřit (myslel jsem, že algebru už jste měli).
Offline
#5 13. 05. 2016 18:04
Re: Polynom
↑ Bati:
tak Euklidův algoritmus samozřejmě znám, nicméně nevím jak to na to napasovat. (máme lineární algebru, algebra jako taková začíná 3. semestr.)
Mám tedy polynom 
a chci ho vydělit polynomem  kde
kde 
Euklidův algoritmus když na toto použiji tak dostanu akorát
a z tohoto něco plyne?
Popřípadě nevíš náhodou o nějakém pěkném důkazu tohoto tvrzení - že to nelze?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 13. 05. 2016 20:06 — Editoval vanok (13. 05. 2016 20:26)
Re: Polynom
Ahoj ↑ Freedy:,
I ked tvoje pohnutky nie su jasne, je pravda, ze iste by si mohol prehlbit tvoje poznatky o polynomov (specialne na faktorialnych okruhoch= Anneaux factoriels) a ak hladas nejake doplnkove citanie o tom, tak preco nie Knuth,the art of computer programing, seminumerical algorithms (1973).
Dobru zabavu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
