Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2016 12:24 — Editoval vanok (03. 04. 2016 11:38)
Vektorovy priestor
Pozdravujem,
Asi kazdeho uz napadla tato otazka:
Existuje vektorovy priestor 
Presnejsie povedane, existuje vonkajsy sucin, 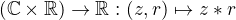 ? (z su skalary, r vektory).
? (z su skalary, r vektory).
Strucne povedane, pre taky sucin ( ak existuje)  je
je 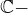 vektorovy priestor.
vektorovy priestor.
Odpoved je: existuje. Len co budem mat trochu casu, popisem jednu takuto strukturu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 26. 04. 2016 23:10 — Editoval vanok (26. 04. 2016 23:14)
Re: Vektorovy priestor
Najprv predpokladajme, ze take vonkajsie nasobenie existuje a definujme 
Polozme  pre
pre 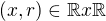 .
.
Potom 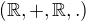 je jeden vektorovy priestor, a
je jeden vektorovy priestor, a  je jeden endomorfismus tohto priestoru taky,ze
je jeden endomorfismus tohto priestoru taky,ze 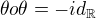 .
.
Naviac pre  mame
mame  .
.
Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 25. 05. 2016 13:03
Re: Vektorovy priestor
Reciprocne.
Nech 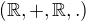 je vektorovy priestor na
je vektorovy priestor na 
a  jeden endomorfismus tohto priestoru taky, ze
jeden endomorfismus tohto priestoru taky, ze 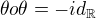 .
.
Definujme externe nasobenie (= nasobenie skalarom) relaciou .
.
Overit, ze pre toto nasobenie  je
je  -vektorovy priestor ( co piseme ako
-vektorovy priestor ( co piseme ako 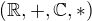 ) je jednoduche, ( urobte to ) az na to ze skutocne treba pouzit
) je jednoduche, ( urobte to ) az na to ze skutocne treba pouzit 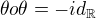 .
.
Cize na do riesenie problemu treba nast taky endomorfismus  .
.
A to je mozne vdaka Hamel-ovym bazam.
Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
