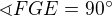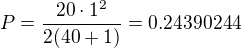Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Výpočet obsahu malého trojúhelníka (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 05. 2016 23:37
Výpočet obsahu malého trojúhelníka
Zdravím.
Vypočítej obsah malého trojúhelníka.
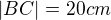
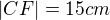
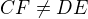
Obrázek je pouze pro představu, tedy výška ve trojúhelníku 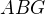 se nedá vypočítat pomocí goniometrické funkce, protože nevíme, kolik bude mít přilehlá strana.
se nedá vypočítat pomocí goniometrické funkce, protože nevíme, kolik bude mít přilehlá strana.
Napadá prosím někoho nějaký způsob?
Všechny mé ztroskotali, po zjištění, že nelze vypočítat výška a že  tam není znova.
tam není znova.
Offline
- (téma jako vyřešené označil(a) Roidoc)
#4 26. 05. 2016 08:46 — Editoval Cheop (26. 05. 2016 12:14)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Výpočet obsahu malého trojúhelníka
↑ Roidoc:
Osobně si myslím, že tak jak je úloha zadána:
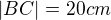
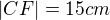

pak bod E splyne s bodem D
PS Po trochu delším uvažování nemá úloha jednoznačné řešení.
V zadání chybí ještě jeden údaj, tzn., že bod E splyne s bodem D je jen jedna z možností.
Nikdo není dokonalý
Offline
#7 29. 05. 2016 08:45 — Editoval misaH (29. 05. 2016 09:33)
- misaH
- Příspěvky: 13459
Re: Výpočet obsahu malého trojúhelníka
↑ Roidoc:
Na OBSAH toho ABCF vôbec AF nepotrebuješ.
Ak by si aj obsah toho lichobežníka vyrátal, načo by ti bol ten rozdiel obsahov?
Podľa Geogebry tá situácia z obrázka neexistuje.
Ak sa obrázok narysuje, nevychádza CF rovné 15 (ak som sa pri zadávaní nepomýlila).
Offline
#8 29. 05. 2016 09:06 — Editoval misaH (29. 05. 2016 09:12) Příspěvek uživatele misaH byl skryt uživatelem misaH.
#11 29. 05. 2016 10:28
Re: Výpočet obsahu malého trojúhelníka
Znovu upozorňuji, že při takto zadaných údajích nemůže být úloha řešitelná. Snad pouze teoreticky.
Zde by muselo platit 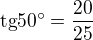 , což neplatí.
, což neplatí.
Při takto zadaném obrázku
by muselo platit 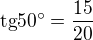 , což neplatí.
, což neplatí.
Jedině, že ABCD není obdélník.
Offline
#20 30. 05. 2016 05:44 — Editoval Al1 (30. 05. 2016 07:29)
Re: Výpočet obsahu malého trojúhelníka
Offline
#21 30. 05. 2016 11:33 — Editoval Honzc (30. 05. 2016 12:47)
Re: Výpočet obsahu malého trojúhelníka
↑ Roidoc:
Jak už bylo řečeno úloha je špatně zadaná.
Budeme předpokládat, že není zadán úhel 50 st. (pak už se dá spočítat)
Postup výpočtu:
1. Spočítáš EF (k výpočtu BE1=CE využiješ funkci tangens)
2. Trojúhelníky ABG a EFG jsou podobné
3. Součet výšek obou trojúhelníků je 20.
Offline
#22 30. 05. 2016 12:20 — Editoval Cheop (30. 05. 2016 12:21)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Výpočet obsahu malého trojúhelníka
↑ Honzc:
Zdravím,
v některm příspěvku zadavatel psal, že křížící se "úhlopříčky" jsou na sebe kolmé.
Pak při ostatním ponechaném zadaní by to vypadalo takto:
a ten malý trojúhelníček by měl obsah
S= 0,2439
Nikdo není dokonalý
Offline
#24 30. 05. 2016 13:43 — Editoval Al1 (30. 05. 2016 13:52)
Re: Výpočet obsahu malého trojúhelníka
↑ Cheop: ↑ Honzc:
Pokud upravíme zadání, pak je úloha řešitelná. Ae to by se dalo udělat s každou úlohou: upravíme rovnici a ta, která by původně neměla řešení, hned řešení má. Číselný výraz má podle výsedků ve sbírce mít hodnotu jedna, jenže nám vychází dva - upravíme zadání a ejhle máme "správné" řešení. Kořeny kvadratické rovnice jsou iracionální, to se nám nelíbí, upravíme rovnici a máme "hezké" celočíselné řešení. To podle mě není správná cesta.
↑ Roidoc:
v jednom tvém příspěvku ti kolegyně ↑ misaH: radila, abys zadával své dotazy přesně. Já se k tomu přikláním.
Offline
#25 30. 05. 2016 15:51
Re: Výpočet obsahu malého trojúhelníka
↑ Al1:
Pardon, ale dotazy zapisuji tak, jak je máme ze školy, já nemůžu zato, že naše p. učitelka si vymyslí příklad a počítáme ho na risk, pokud to nejde, tak si něco domyslíme. Naše p. učitelka nemá vystudovanou matematiku, ona se jí učila sama, takže bych se ani nedivil, kdyby některé příklady byly špatně nebo nešly vypočítat.
↑ Cheop:
A tohle je třeba krásné řešení, dokonce jsem i psal, že tam je  a pokud to tak je, pak výsledek, který jim vyšel ve škole (t.j.
a pokud to tak je, pak výsledek, který jim vyšel ve škole (t.j. 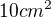 ) je špatně.
) je špatně.
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Výpočet obsahu malého trojúhelníka (TOTO TÉMA JE VYŘEŠENÉ)
 a
a  vypočítat dokážu.
vypočítat dokážu.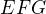 , platí totiž
, platí totiž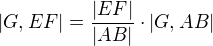 a
a 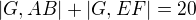 .
.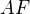 , vypočítat obsah
, vypočítat obsah 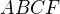 a odečíst obsah
a odečíst obsah  ?
?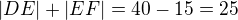
 (obsah)
(obsah)