Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sobolevův prostor - definice (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2016 16:32
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Sobolevův prostor - definice
Ahoj všichni!
Dneska jsem narazil na definici Sobolevova prostoru:
Máme normu .
.
Sobolevův prostor  je pak zúplnění prostoru
je pak zúplnění prostoru  .
.
Nejsem si vůbec jistý, jestli tohle chápu dobře... Jde o to, že Sobolevův prostor je prostor funkcí s normou  a všechny její prvky (funkce) mají spojité všechny derivace?
a všechny její prvky (funkce) mají spojité všechny derivace?
Offline
- (téma jako vyřešené označil(a) Katsushiro)
#2 10. 06. 2016 18:28 — Editoval Bati (10. 06. 2016 21:20)
Re: Sobolevův prostor - definice
Ahoj ↑ Katsushiro:,
uvědom si, že ne všechny prostory s normou jsou úplné. Třeba prostor ![kopírovat do textarea $C^1([-1,1],\lVert\cdot\rVert_{0})$](/mathtex/1c/1ce191ce6b7391010bfd3c68aa18ec03.gif) , kde
, kde ![kopírovat do textarea $\lVert f\rVert_{0}:=\sup_{x\in[0,1]}|f(x)|$](/mathtex/6d/6d2000d580efe87fe0d2bed717b5b42a.gif) není úplný. Můžeš totiž najít posloupnost v
není úplný. Můžeš totiž najít posloupnost v  , která v normě
, která v normě  (tj. stejnoměrně) konverguje např. k funkci
(tj. stejnoměrně) konverguje např. k funkci 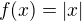 , která nemá derivaci v nule. Jsou 2 možnosti, jak to spravit.
, která nemá derivaci v nule. Jsou 2 možnosti, jak to spravit.
1) Vzít správnou normu. Z předchozího protipříkladu je zřejmé, že je třeba zohlednit fční hodnoty i derivace, takže definjeme  . Pak už prostor
. Pak už prostor ![kopírovat do textarea $C^1([-1,1],\lVert\cdot\rVert_1)$](/mathtex/8e/8e2c9cc061fe7d5510b43604234ee4eb.gif) je úplný (tj. Banachův).
je úplný (tj. Banachův).
2) Prostor ![kopírovat do textarea $C^1([-1,1],\lVert\cdot\rVert_{0})$](/mathtex/1c/1ce191ce6b7391010bfd3c68aa18ec03.gif) zúplníme, tj. vezmeme
zúplníme, tj. vezmeme ![kopírovat do textarea $X:=\overline{C^1([-1,1])^{\quad\lVert\cdot\rVert_0}}$](/mathtex/e8/e81eebaef2bb70e91c3dff8c46949e7b.gif) . Měl bys nahlédnout, že
. Měl bys nahlédnout, že ![kopírovat do textarea $X=C^0([-1,1],\lVert\cdot\rVert_0)$](/mathtex/27/27ae1269dafa716eb7b722f53ed61bd1.gif) .
.
Nyní k tvému konkrétnímu problému. O prostoru  je známo, že není úplný vzhledem k žádné normě (je to totiž jen Fréchetův prostor), takže zbývá možnost 2). Platí tedy
je známo, že není úplný vzhledem k žádné normě (je to totiž jen Fréchetův prostor), takže zbývá možnost 2). Platí tedy  . Rozhodně to ale neznamená, že každá Sobolevovská funkce je hladká, znamená to jen, že ke každé Sobolevovské funkci můžeme najít posloupnost hladkých funkcí, která k ní konverguje v
. Rozhodně to ale neznamená, že každá Sobolevovská funkce je hladká, znamená to jen, že ke každé Sobolevovské funkci můžeme najít posloupnost hladkých funkcí, která k ní konverguje v  normě. To je ale velmi významná vlastnost, která se používá k důkazu různých vlastností Sobolevovských funkcí (rozšíření, vnoření, stopa ...).
normě. To je ale velmi významná vlastnost, která se používá k důkazu různých vlastností Sobolevovských funkcí (rozšíření, vnoření, stopa ...).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sobolevův prostor - definice (TOTO TÉMA JE VYŘEŠENÉ)