Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » DIM na jaderce (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 04. 2009 17:24 — Editoval Ninkasu (27. 04. 2009 17:29)
DIM na jaderce
Nekteré příklady z hodin diskrétní matematiky na jaderce. Popravde tomu moc nerozumim tak kdyz nekdo napise reseni s postupem budu rad, nicmene to sem davam hlavne pro ty co si radi pocitaji. Budu tenhle topic aktualizovat co to půjde :)
některé jsou již zde: Odkaz
1.
Dokažte, že jsou-li  , a + b takové, že
, a + b takové, že  , pak c = a + b
, pak c = a + b
2.
Dokažte, že  kořeny
kořeny  polynomu
polynomu  splňují
splňují 
3.
Najděte kubický polynom, jekož kořeny jsou druhé mocniny kořenů polynomu 
Offline
#3 27. 04. 2009 17:32 — Editoval Pavel (27. 04. 2009 17:33)
Re: DIM na jaderce
↑ Ninkasu:
ad 2) stačí uvažovat rovnici 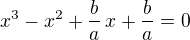 a spolu s ní Vietovy vztahy mezi kořeny a koeficienty rovnice. A je to.
a spolu s ní Vietovy vztahy mezi kořeny a koeficienty rovnice. A je to.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 27. 04. 2009 18:58
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: DIM na jaderce
Ad 1)c=a+b+e
(a+b)^3+3(a+b)^2e+3(a+b)e^2+e^3=(a+b)^3+3abe
3(a+b)^2e+3(a+b)e^2+e^3=3abe
Pokud e není 0
3(a+b)^2+3(a+b)e+e^2=3ab
e^2+3(a+b)e+3(a+b)^2-3ab=0
Řešeme jako kvadratickou rovnici pro e. Diskriminant je
9(a+b)^2-12(a+b)^2+12ab=-3a^2+6ab-3b^2=-3(a+b)^2.
Pokud je a+b různé od 0, žádné e nenajdeme, pro a=-b máme e^2+3a^2=0, jediné řešení e=0.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 27. 04. 2009 23:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: DIM na jaderce
Ad 3)
Kořeny polynomu  označím
označím  ,
,  a
a 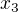 . Napíšu si Vietovy vztahy:
. Napíšu si Vietovy vztahy:
Obě strany každé rovnice umocním na druhou
a použiju uvedené Vietovy vztahy.
Hledaný kubický polynom je tedy .
.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » DIM na jaderce (TOTO TÉMA JE VYŘEŠENÉ)