Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 06. 2016 21:34
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Goniometrická rovnice
↑ _Mitsuki: Ahoj,
využi, že platí: 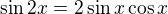
Offline
#4 12. 06. 2016 22:07
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Goniometrická rovnice
↑ Maty1a: Ahoj,
tvoje riešenie je samozrejme správne. Ale je dosť možné, že ↑ _Mitsuki: by ho našla aj sama len s pomocou vzorca, ktorý som uviedla vyššie. Je lepšie pokúsiť sa druhého človeka nasmerovať, ako mu hneď položiť na tácku kompletné riešenie. Kompletné riešenie môže priniesť plný počet bodov z domácej úlohy, ale nemusí vždy priniesť aj pochopenie postupu, akým sa úlohy takéhoto typu riešia. Na fóre sa riadime určitými pravidlami, toto je jedno z nich.
Offline
#7 12. 06. 2016 22:16
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Goniometrická rovnice
↑ _Mitsuki: Ja to skôr chápem ako počet riešení v danom intervale, sú dve.
Offline
#9 12. 06. 2016 22:24
Re: Goniometrická rovnice
↑ Blackflower:
Ano, ale v zadání chtějí součet všech řešení
jsou tam možnosti:
a)pi/2 b) pi c pi/3 d)pi/6 e)jiná odpověď
Správná odpověď je a), ale nechápu jak...
Offline
#10 12. 06. 2016 22:25
#12 12. 06. 2016 22:26
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Goniometrická rovnice
↑ _Mitsuki: Tak potom sa pozri na to, čo ti napísala ↑ gadgetka: a vyjde ti presne a).
Offline
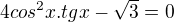
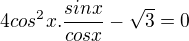
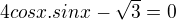


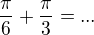
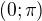 .
.