Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Výška v trojúhelníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 06. 2016 19:05
Výška v trojúhelníku
Ahoj. Pracuji na svém projektu, který se týká výšky v trojúhelníku. V jakémkoliv. Dejme tomu, že máme libovolný trojúhelník ABC, kde c je nejdelší strana. Vím, že výška na tuto stranu dělí trojúhelník na dva pravoúhlé (a stranu c na x a y) a pomocí Pythagora se dá k této výšce, jestli známe všechny strany, dopočítat:
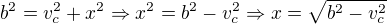

Nakonec vyjde:
Tuto rovnici jsem vyzkoušel na několika různých trojúhelnících a rýsováním jsem si ověřil, že výpočet je správný. Nedávno mě ale napadlo, že bych mohl z té rovnice utvořit přímo vzorec "v = něco něco". Ale narazil jsem na problém. Výpočtem jsem se dostal k tomuto výrazu: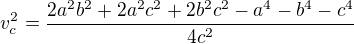
Upřímně, takový vzorec vypadá dost nelidsky a já si s ním neumím poradit. Tak vás tedy prosím, jestli byste mi nemohli pomoct s tím to dál zredukovat. I učitelka mi řekla, ať se obrátím na pomoc na internetu, sama říkala, že jí to jednou pomohlo. Děkuji vám tedy pěkně. Sem ještě dodám celý postup, jak jsem k oné rovnici přišel.



(roznásobování čtyřčlenu vynechám, pokračuji stavem po vykrácení)

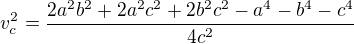
Offline
- (téma jako vyřešené označil(a) Skippy)
#2 12. 06. 2016 19:33
Re: Výška v trojúhelníku
Ahoj,
na první pohled tam nevidím žádnou chybu, ale nekontroloval jsem to úplně pečlivě. Čím jsem si ale jistý je to, že ten vzorec nevypadá nelidsky, naopak přesně něco takového lze očekávat. Proč? V podstatě jsi totiž dokázal Heronův vzorec pro výpočet obsahu trojúhelníka pomocí délky jeho stran. Srovnej s
https://cs.wikipedia.org/wiki/Heron%C5%AFv_vzorec
a členy v tom vzorci roznásob.
Offline
#4 13. 06. 2016 22:27
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Výška v trojúhelníku
Ahoj,
viz https://www.wolframalpha.com/input/?i=( … 2F(4c%5E2).
Ta druhá úprava opravdu silně připomíná Heronův vzorec.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Výška v trojúhelníku (TOTO TÉMA JE VYŘEŠENÉ)
