Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Curve Fitting v MATLABe - zobrazovanie koeficientov (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 06. 2016 10:10
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Curve Fitting v MATLABe - zobrazovanie koeficientov
Po dlhej dobe opäť zdravím.
Dostal som úlohu pofitovať experimentálne dáta v MATLABe. Bohužiaľ s ním robím veľmi zriedka, naposledy som ho použil cca pred dvoma rokmi a preto mi veľa vecí a fukcií v ňom uniká. Mám exp. dáta, ktoré by mali byť fitované touto funkciou:
Vzhľadom na charakter mojich dát je veľký rádový rozdiel medzi hodnotami koeficentov - koeficianty A, B sú rádu 10^-2 až 10^-1, koeficient C je rádu 10^4 (nie je to chyba, taký je očakávaný výsledok).
Skúšal som na to použiť Curve Fitting app - nahodil som dáta, vytvoril custom function a dáta mi odfitovalo, ale v Results okne mám problém s tým, ako sa mi koeficienty zobrazujú. A a B sú ako desatinné čísla iba so štyrmi des. miestami, koeficient C je scientific a zaokrúhľuje mi ho na desiatky (je v tvare X.XXXe+04). U A,B sa to jakž-takž dá akceptovať, ale C je v tomto nepresnom tvare pre mňa bezcenné.
Hľadal som, ako upraviť zobrazovanie significant digits, ale priamo v Curve Fittingu som to nikde nenašiel a ani na internete som nebol úspešný. Pri nahadzovaní dátových súborov do MATLABu som mal formát nastavený na longEng. Ako ten program "dokopať" k tomu, aby mi koeficienty zobrazoval správne? Potreboval by som aspoň 5 des. miest u každého.
Offline
- (téma jako vyřešené označil(a) Ferdish)
#3 14. 06. 2016 08:30
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Ferdish:
Ahoj, s Matlabem nepracuji, takže spíše jen obecně: Současného výpočtu koeficientů lišících se o pět resp. šest řádů bych se docela bál, to už si koleduješ o to, aby ti nafackovala zaokrouhlovací chyba. Takže bych nejprve vypočítal konstantu C. To není težké, pokud jsem se zamyslel dobře a pokud minimalizuješ kvadratickou odchylku, je to prostě aritmetický průměr změřených hodnot. To bys měl mít přesnost výpočtu snadno pod kontrolou. Potom přejdeš od původní datové řady s prvky fi k datové řadě: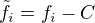
Teprve tuto datovou řadu si fituj funkcí:
Možná to všechno Matlab ošetřuje a tohle je zbytečné. Ale když jsi nic nenašel, předpokládám, že informace o tom je skryta v hlubinách podrobného manuálu ;-)
Доктор сказал «в морг» — значит в морг!
Offline
#4 14. 06. 2016 09:49
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
ahoj ↑ Ferdish:,
nespoléhal bych na nějaký vestavěný fitting a proložil sám - metodou nejmenších čtverců.
Budoucnost patří aluminiu.
Offline
#5 14. 06. 2016 12:15
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
Formol napsal(a):
Takže bych nejprve vypočítal konstantu C. To není težké, pokud jsem se zamyslel dobře a pokud minimalizuješ kvadratickou odchylku, je to prostě aritmetický průměr změřených hodnot.
Nejako mi uniká myšlienkový postup toho, ako môžem pomocou metódy jednoduchého aritmetického spriemerovania nameraných hodnôt dospieť ku hodnote konštanty  . Môžeš to trochu rozviesť, prosím?
. Môžeš to trochu rozviesť, prosím?
Offline
#6 14. 06. 2016 12:56
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Ferdish:
Prostě máš nějakou množinu naměřených hodnot fi, kterou si chceš aproximovat konstantní funkcí f(x)=C.
Součet kvadratických odchylek (metoda nejmenších čtverců) je definován: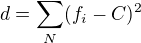
Odchylku chci minimalizovat, tedy zjistit, pro jaké C má funkce d(C) minimum. Zřejmě tam bude mít nulovou derivaci, tedy: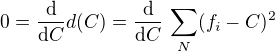
Derivovat konečnou sumu jde vždy člen po členu, tedy po derivování: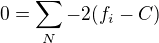
Po jednoduché úpravě je:
a to už jde přeskupit: 
a tedy:
No a to není nic jiného než aritmetický průměr hodnot fi.
____________________________
Nezaručuji, že výsledná aproximace nebude mít problémy v tom smyslu, že v konečném důsledku nebude minimalizovat kvadratickou odchylku. Dokonce bych si byl skoro jistý tím, že nebude, ale nechce se mi to dokazovat/ověřovat. Ale protože máš požadované koeficienty odlišné o pět resp. šest řádů, měla by tě trápit spíše propagace chyb při zaokrouhlování. Tedy pokud nechceš zabřednout do hlubších partií aproximace a najít si nějaké čistší řešení..
Доктор сказал «в морг» — значит в морг!
Offline
#7 14. 06. 2016 14:29 — Editoval Eratosthenes (14. 06. 2016 14:46)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Formol: ↑ Ferdish:
takže mám tabulku
xi -3 -2 -1 0 1 2 3
yi 10 5 2 1 2 5 10
a potřebuju tím proložit parabolu Ax^2 + C
Vaší "metodou" nejdřív "fituju na C" - aritm. průměr je 5, tj. C=5. Takže parabola bude tvaru Ax^2 + 5.
To myslíte opravdu vážně?
Budoucnost patří aluminiu.
Offline
#8 14. 06. 2016 14:47
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Ferdish:
Chceš jenom spočítat tento konkrétní příklad, anebo pochopit metodu?
Budoucnost patří aluminiu.
Offline
#9 14. 06. 2016 16:09
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Eratosthenes:
To myslím vážně v tomto případě, kdy je absolutní člen ve fitující funkci o několik řádů vyšší než ostatní koeficienty. Hlavním problémem je v tomto případě zaokrouhlovací chyba, proto navrhuji nejjednodušší postup, který povede k řešení, které v daném případě bude (nejspíš) dávat použitelné výsledky. Váš "protipříklad" se proto dokonale míjí s podstatou problému.
Доктор сказал «в морг» — значит в морг!
Offline
#10 14. 06. 2016 17:52
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Formol:
dobrá, tak tedy abych "neminul podstatu problému":
xi -900 -600 -300 0 300 600 900
yi 1810 1360 1090 1000 1090 1360 1810
koeficienty paraboly se liší o šest řádů přesně jako v příkladě a postup s průměrem je úplně stejně blbě...
Prostě mu říkáš - když je ten absolutní člen tak velký, tak se na ostatní koeficienty prostě vykašli a flákni tam aritmetický průměr. U ostatních koeficientů pak už můžou být paraboly exponenciály, sinusoidy, anebo třeba funkce gama. Je to jedno, protože je-li C aritmetický průměr, pak ty ostatní koeficienty stejně vždycky vyjdou nula.
Konec konců - aj tak možno...
Budoucnost patří aluminiu.
Offline
#11 14. 06. 2016 18:50
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Formol:
Teraz už chápem. Z fyzikálneho hľadiska je však tento postup nepoužiteľný.
Asi som najprv mal spomenúť, o aké dáta vlastne ide. Keďže tie dáta nemôžem len tak zvereniť resp. referovať o čo ide, poviem len to najnutnejšie.
Jedná sa o slabú, ale citlivú závislosť veličiny  od teploty, nameranú v subkelvinovej (1 mK - 1 K) teplotnej oblasti. Fitovacia funkcia potom prejde na tvar
od teploty, nameranú v subkelvinovej (1 mK - 1 K) teplotnej oblasti. Fitovacia funkcia potom prejde na tvar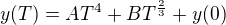
pričom hodnoty teplôt sú dosadzované v kelvinoch. S ohľadom na odhad koeficientov si určite dokážete predstaviť, aká malá je veľkosť zmeny tejto veličiny s teplotou a teda prečo chcem tie koeficienty určiť tak presne. Preto som sa spoliehal na software MATLABu, pretože som myslel že keď pr načítavaní dáit mu zadám format longEng, tak že to CF dokáže spočítať dostatočne presne. Teraz aspoň viem, že to bolo bláhové.
Zrejme mi neostáva nič iné, ako to riešiť "manuálne" cez najmenšie štvorce, tak ako to navrhoval ↑ Eratosthenes: Nikdy som to síce nerobil, natož v MATLABe (viem, znie to absurdne a alibisticky, ale je to pravda), ale čo - všetko je raz po prvýkrat.
Môžem na to napr. použiť definovaný postup v týchto skriptách od strany 35, pričom môžem za aproximačnú funckiu zvoliť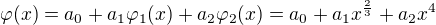
a váhovú funckiu 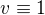 . Pochopil som to správne?
. Pochopil som to správne?
Offline
#12 14. 06. 2016 19:01
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
ahoj ↑ Ferdish:
>> Môžem na to napr. použiť definovaný postup v týchto skriptách od strany 35
Ano, je to tak.
Budou-li nějaké problémy, ozvi se.
Budoucnost patří aluminiu.
Offline
#13 14. 06. 2016 19:07
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
No a je to nutné použít Matlab?
Nestačí to spočítat v Excelu? Má zabudovanou funkci linest, která to umí. Nebo můžeš použít řešitele - ten to také zvládne.
Offline
#14 14. 06. 2016 19:48
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ mák: Matlab nie je nevyhnutnosť, ale je to jeden z programovacích jazykov, čo ovládam.
Ad Linest - ten aproximuje len priamkou, nie? Ja to potrebujem fitovať práve tým polynómom, ktorý mám v zadaní.
Offline
#15 14. 06. 2016 19:50
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
Samozřejmě umí i libovolný polynom, jenom se mu to musí správně napsat.
Offline
#16 14. 06. 2016 19:59
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ mák:
není polynom.
Budoucnost patří aluminiu.
Offline
#17 14. 06. 2016 20:49
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Ferdish:
% sem dej svoje data
X=[ 1 2 3 4 5 6];
Y=[-95 -63 68 420 1160 2500];
fi0=ones(1,length(X))
fi1=X.^(2/3)
fi2=X.^4
A=[dot(fi0,fi0) dot(fi0,fi1) dot(fi0,fi2);
dot(fi1,fi0) dot(fi1,fi1) dot(fi1,fi2);
dot(fi2,fi0) dot(fi2,fi1) dot(fi2,fi2)];
b=[dot(Y,fi0);
dot(Y,fi1);
dot(Y,fi2)]
a=A\b
% a tady to máš i s obrázkem...
figure
grid on
hold on
plot(X,Y,'ro')
x=X(1):0.1:X(length(X));
Funkce=a(1)+a(2)*x.^(2/3)+a(3)*x.^4;
plot(x,Funkce)
Budoucnost patří aluminiu.
Offline
#18 14. 06. 2016 21:07
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Eratosthenes:
To je jedno, stejně to spočítá.
Offline
#19 15. 06. 2016 08:53
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Curve Fitting v MATLABe - zobrazovanie koeficientov
↑ Eratosthenes:
To si ani nemusel, prišiel by som na to po čase sám, ale díky!
Reputace +
Offline
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Curve Fitting v MATLABe - zobrazovanie koeficientov (TOTO TÉMA JE VYŘEŠENÉ)