Matematické Fórum

Archer785 · 20. 06. 2016 20:45

Zdravím,

mohl by mi někdo vysvětlil proč a jak se sestavuje ta výsledná soustava rovnic ? Řešení zvládám, jen tady u toho sestavení si nejsem jistej.

Díky moc

//forum.matweb.cz/upload3/img/2016-06/48209_Untitled.png

Pritt · 21. 06. 2016 10:14 — Editoval Pritt (21. 06. 2016 10:28)

↑ Archer785:

Ahoj, když označím $\vec x_1 = \begin{pmatrix} 1 \\ 1\\ -1 \\ 0\end{pmatrix}, \; \vec x_2 = \begin{pmatrix} 1 \\ 2\\-1\\-2\end{pmatrix}, \; \vec x_3 = \begin{pmatrix}1\\0\\0\\1 \end{pmatrix}, \; \vec x_4 = \begin{pmatrix} 1\\1\\1\\1\end{pmatrix}$ .

Potřebuješ sestavit matici lineárního zobrazení ve standardních bázích $^{\epsilon_4}A^{\epsilon_3}$ .

i-tý sloupec matice A je tvořen obrazem i-tého vektoru ze standardní báze $\epsilon_4$ při zobrazení $A$ (se souřadnicemi v bázi $\epsilon_3$ ).

Rozepsáno po sloupcích:

$^{\epsilon_4}A^{\epsilon_3}=((A(\vec e_1))_{\epsilon_3}\; (A(\vec e_2))_{\epsilon_3}\; (A(\vec e_3))_{\epsilon_3}\; (A(\vec e_4))_{\epsilon_3} )$ .

Pro sestavení takové matice potřebuješ tedy znát obrazy vektorů ze standardní báze $\epsilon = (\vec e_1,\vec e_2,\vec e_3,\vec e_4)$ .

Znáš ale jen obrazy vektorů $\vec x_1, \vec x_2,\vec x_3,\vec x_4$

Tyto vektory lze zapsat takto:

$\vec x_1 = 1\cdot \vec e_1 + 1\cdot \vec e_2 + (-1)\cdot \vec e_3 + 0\cdot \vec e_4 \nl \vec x_2 = 1\cdot \vec e_1 + 2\cdot \vec e_2 + (-1)\cdot \vec e_3 + (-2)\cdot \vec e_4 \nl \vec x_3 = 1\cdot \vec e_1 + 0\cdot \vec e_2 + 0\cdot \vec e_3 + 1\cdot \vec e_4 \nl \vec x_4 = 1\cdot \vec e_1 + 1\cdot \vec e_2 + 1\cdot \vec e_3 + 1\cdot \vec e_4$

Musíš tedy vyjádřit $\vec e_i, \; i \in \{1,2,3,4\}$ jako lineární kombinaci $\vec x_1,\vec x_2,\vec x_3,\vec x_4$ .

Takže stačí sestavit matici $(\vec x_1,\vec x_2,\vec x_3,\vec x_4 | \vec e_1,\vec e_2,\vec e_3,\vec e_4)$

Výsledné řešení pak počítáš pro každý sloupec na pravé straně zvlášť.

Dostaneš například $\vec e_1 = \sum_{i=1}^{4} \alpha_i \vec x_i$ tedy jako lineární kombinaci $\vec x_1,\vec x_2,\vec x_3,\vec x_4$ . Protože máme ale zobrazení lineární, platí to samé i pro jejich obrazy.

Tedy $A(\vec e_1) = A(\sum_{i=1}^{4} \alpha_i \vec x_i) = A(\alpha_1\vec x_1+\alpha_2\vec x_2 + \alpha_3\vec x_3 + \alpha_4\vec x_4) = \nl =A(\alpha_1\vec x_1)+A(\alpha_2\vec x_2) +A( \alpha_3\vec x_3) + A(\alpha_4\vec x_4) = \alpha_1 A(\vec x_1)+\alpha_2 A(\vec x_2) +\alpha_3 A( \vec x_3) + \alpha_4 A(\vec x_4)$ .

Teď můžeš sestavit matici $A$ a najít partikulární řešení. Jádro zobrazení hledat nemusíš, vektory z jádra jsou v zadání.

vanok · 21. 06. 2016 12:54

Ahoj ↑ Pritt:,
Male poznamky
Prejst do standarnych baz nie je povinne. Ale je To v niecom pohodlne.

Co pises o jadre tu plati (preco?) ale nie je to platne vseobecne.

Dobre pokracovanie.

Pritt · 21. 06. 2016 13:48 — Editoval Pritt (21. 06. 2016 13:50)

Zdravím ↑ vanok:

Zapomněl jsem to napsat, tady to platí, protože hodnost zobrazení A, h(A) = 2, tzn, že defekt d(A) = 2. V zadání máme zadané dva lineárně nezávislé vektory, které se zobrazují na nulový vektor z 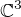$\mathbb{C}^3$ . Tedy už nemusíme hledat další LN vektory z jádra, protože jich více není.

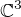Druhého postupu jsem si vědom. Tedy využít toho, že $A\vec x = b \Leftrightarrow (A\vec x)_y = (\vec b)_y \Leftrightarrow \;\;^xA^y(\vec x)_x = (\vec b)_y$ . Kde $X$ je báze $\mathbb{C}^4$ a $Y$ báze $\mathbb{C}^3$ . Zkoušel jsem to, ale nevycházela pěkná čísla, tak jsem upřednostnil postup s maticí ve standardních bázích.

Matematické Fórum

#1 20. 06. 2016 20:45

Zobrazení - hledání řešení rovnic

#2 21. 06. 2016 10:14 — Editoval Pritt (21. 06. 2016 10:28)

Re: Zobrazení - hledání řešení rovnic

#3 21. 06. 2016 12:54

Re: Zobrazení - hledání řešení rovnic

#4 21. 06. 2016 13:48 — Editoval Pritt (21. 06. 2016 13:50)

Re: Zobrazení - hledání řešení rovnic

Zápatí