Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypočíst integrál substituční metodou (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 06. 2016 17:21 — Editoval Lobacho (28. 06. 2016 17:21)
Vypočíst integrál substituční metodou
Zdravím,
snažím se vypočítat tento příklad: ,
,
má to jít substituční metodou. S tou jsem však byl bezradný. Objevil jsem však to, že je ten příklad velmi podobný jednomu ze základních vzorců pro výpočet neurčitých integrálů:
a je mu podobný v tom, že má jen dvojnásobný argument:
Dotaz ode mě, měl by tedy výsledek být:  ?
?
V klíči v učebnici je napsáno, že správně je  , já nemohu přijít na to, kde se tam ta jedna polovina vzala.
, já nemohu přijít na to, kde se tam ta jedna polovina vzala.
Předem děkuji za radu
Supervisor: Attention, whoever you are, this channel is reserved for emergency calls only.
John McClane: No f*cking sh*t, lady. Does it sound like I'm ordering a pizza?
Offline
- (téma jako vyřešené označil(a) Lobacho)
#4 28. 06. 2016 17:37
Re: Vypočíst integrál substituční metodou
↑ Lobacho:
Dobrý den,
po jednoduché úpravě výrazu pod odmocninou zkuste substituci: 
Offline
#5 28. 06. 2016 18:10
Re: Vypočíst integrál substituční metodou
↑ Kenniicek:
děkuji, zpětně jsem derivoval a je to pak jasné že tam ta 1/2 musí bejt, ale pořád mi nedochází jak k tomu dojít přes integraci
↑ Xellos:
když používám substituci tak mám 

a s tím se přeci nedá pracovat. Na situace, když je ve jmenovateli polynom třeba 2. řádu, se používá rozklad na parciální zlomky, ale ten zase nejde provést tady, protže tam je ta odmocnina. Můžte být konkrétnější prosím?
↑ Takjo:
nechápu jak mám provést substituci
takto? : 

Supervisor: Attention, whoever you are, this channel is reserved for emergency calls only.
John McClane: No f*cking sh*t, lady. Does it sound like I'm ordering a pizza?
Offline
#6 28. 06. 2016 18:14
Re: Vypočíst integrál substituční metodou
↑ Lobacho:
Ano, přesně tak.
A pak se vraťte k původní proměnné: 
Offline
#7 28. 06. 2016 18:19
Re: Vypočíst integrál substituční metodou
↑ Lobacho:
Substitucia v tomto pripade bude:


Ale my nemame 2dx ale len jedno, preto:
A preto je tam ta jedna polovica vo vysledku :)
Offline
#9 28. 06. 2016 18:47
Re: Vypočíst integrál substituční metodou
↑ Kenniicek:
↑ Akojeto:
takže substituce 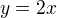 místo toho mého nešikovného
místo toho mého nešikovného 
měl jsem napsat na začátku, co jsem volil za substituci, v té byla moje chyba
děkuji vám
↑ Takjo:
omlouvám se, Vašemu postupu nerozumím, ale děkuji za snahu o pomoc,
po substituci, kterou jste mi potvrdil jako správnou mi výpočet vyšel takto:
což znamená, že jsem asi někde něco nepochopil
Supervisor: Attention, whoever you are, this channel is reserved for emergency calls only.
John McClane: No f*cking sh*t, lady. Does it sound like I'm ordering a pizza?
Offline
#10 28. 06. 2016 19:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vypočíst integrál substituční metodou
Zdravím,
↑ Lobacho: návrh od kolegy ↑ Takjo: a ve Tvé úpravě povede na  , pro
, pro  dává
dává  a dokončit dle kolegy ↑ Takjo: (tato úprava by měla odpovídat i def. oboru původně zadané funkce, ale při substitucích (a na to se občas zapomíná) je dobré vždy kontrolovat, zda navrhovaná substituce nepožaduje omezení na def. obor. V pořádku? Děkuji.
a dokončit dle kolegy ↑ Takjo: (tato úprava by měla odpovídat i def. oboru původně zadané funkce, ale při substitucích (a na to se občas zapomíná) je dobré vždy kontrolovat, zda navrhovaná substituce nepožaduje omezení na def. obor. V pořádku? Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypočíst integrál substituční metodou (TOTO TÉMA JE VYŘEŠENÉ)


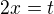
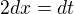 , takže.
, takže. 