Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 07. 2016 15:03
Dalsie prazdninove cvicenie
Nech 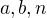 su nenulove prirodzene cisla. Dokazte, ze cislo
su nenulove prirodzene cisla. Dokazte, ze cislo  je cele len pre konecne mnoho cisiel
je cele len pre konecne mnoho cisiel  (D.J.Newman)
(D.J.Newman)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
- (téma jako nevyřešené označil(a) vanok)
#2 03. 07. 2016 00:05
Re: Dalsie prazdninove cvicenie
Už sice nejsem středoškolák, ale stejně sem napíši mou myšlenku. Je pozdě, třeba jsem to celé uchopil nějak úplně špatně. Každopádně jsem zvědav na nějaká hezčí / kratší řešení.
Offline
#3 03. 07. 2016 12:50 — Editoval vanok (03. 07. 2016 20:51)
Re: Dalsie prazdninove cvicenie
Ahoj ↑ liamlim:,
Dam tu riesene na ktore som myslel
Ako sa ti paci tento dokaz?
Daju sa urobit aj ine dokazy...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 03. 07. 2016 20:16
Re: Dalsie prazdninove cvicenie
Jistě je to jednodušší. Já jsem si ten příklad spočítal vlastně jen z důvodu, že teď řeším velmi podobné věci (součet dvou  -tých mocnin (dělitele takových čísel)
-tých mocnin (dělitele takových čísel)
pozn. V důkaze je jistě překlep, nemá tam jistě být  . Jinak pěkný důkaz.
. Jinak pěkný důkaz.
Offline
#5 03. 07. 2016 20:55
Re: Dalsie prazdninove cvicenie
↑ liamlim:,
Ahoj, ano to Y bol preklep dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 ,
,  existuje nekonečně mnoho
existuje nekonečně mnoho  pro nějaké celé
pro nějaké celé  . Ekvivalentně
. Ekvivalentně 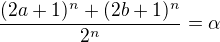 .
.  a liché
a liché  tak, že
tak, že 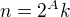 . Po dosazení dostaneme
. Po dosazení dostaneme  . Protože je
. Protože je  . Přitom levý je nutně celé číslo, což plyne z lichosti
. Přitom levý je nutně celé číslo, což plyne z lichosti  . Zbývá ověřit, jestli existuje nekonečně mnoho lichých
. Zbývá ověřit, jestli existuje nekonečně mnoho lichých 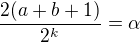 pro nějaké celé
pro nějaké celé 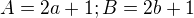 ktore su neparne kladne cisla.
ktore su neparne kladne cisla.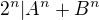 .
.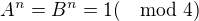 . Tak
. Tak 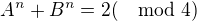 , co da, ze nie je delitelne 4.
, co da, ze nie je delitelne 4.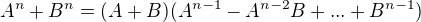
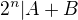 a takych n mozme mat len konecny pocet.
a takych n mozme mat len konecny pocet.