Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obor existence momentové vytvořující funkce
#1 10. 08. 2016 02:34
Obor existence momentové vytvořující funkce
Dobrý den,
Rád bych poprosil o radu. V souvislosti se studiem náhodných procesů mi v posledních dnech vrtá hlavou následující problém:
Mějme nezápornou náhodnou proměnnou 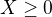 .
.
Potom samozřejmě ![kopírovat do textarea $E[e^{zX}]$](/mathtex/7c/7c3bd9eeaa7c10f7178bd7472a6029df.gif) existuje (a je konečná) na
existuje (a je konečná) na  .
.
Navíc lze dokázat, že ![kopírovat do textarea $z \mapsto E[e^{zX}]$](/mathtex/37/3748dafbd246bb8a5b25b9566cca5bdf.gif) je holomorfní na
je holomorfní na 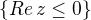 .
.
Předpokládejme, že existuje holomorfní funkce  definovaná na množině větší než
definovaná na množině větší než 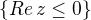 , tj. např. na
, tj. např. na  , a taková, že
, a taková, že ![kopírovat do textarea $f(z) = E[e^{zX}]$](/mathtex/30/305d70330e6d99b7f3360c788059921c.gif) na
na 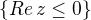 .
.
Lze z toho dokázat, že ![kopírovat do textarea $E[e^{zX}]$](/mathtex/7c/7c3bd9eeaa7c10f7178bd7472a6029df.gif) existuje na
existuje na  ?
?
Děkuji mnohokrát za odpovědi.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Obor existence momentové vytvořující funkce
