Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Gravitace a padajici telesa. (TOTO TÉMA JE VYŘEŠENÉ)
#3 18. 08. 2016 18:51
Re: Gravitace a padajici telesa.
↑ zdenek1:
děkuji za odkaz. Otázka je spíše teoretická a rozluštitelná výpočtem, ne pokusem. Obě najednou nedopadnou..Takže?
Offline
#4 19. 08. 2016 19:17 — Editoval Eratosthenes (19. 08. 2016 19:19)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Gravitace a padajici telesa.
↑ pavoda:
>> Obě najednou nedopadnou...Takže?
Takže ses díval opravdu špatně. Tento slavný pokus provedli dokonce i Američané na Měsící jako poctu Galileo Galileimu, který jako první přišel na to, že ve stejném gravitačním poli padají všechna tělesa stejně rychle (nejsou-li vystavena odporu prostředí).
"Rozluštitelnost výpočtem" je velmi jednoduchá: vezměme těleso o libovolné hmotnosti m (může to být peříčko, anebo třeba náklaďák) a pusťme ho z výšky na zem. Podle Newtonova zákona síly má toto těleso tíhu
kde g je tíhové zrychlení, tedy zrychlení volného pádu.
Podle gravitačního zákona na sebe vzájemně působí náklaďák (peříčko) a Země silou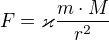
kde 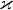 je gravitační konstanta, M hmotnost Země a r vzdálenost těžišť obou těles
je gravitační konstanta, M hmotnost Země a r vzdálenost těžišť obou těles
Protože musí být G=F, je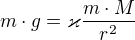
a hmotnost tělesa (m), na kterém má údajně něco záviset, se vykrátí. Takže ať je hmotnost m tělesa jaká chce, gravitace mu vůči Zemi uděluje zrychlení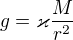
které nezávisí ani na hmotnosti padajícího tělesa, ani na jeho velikosti. Závisí pouze na na hmotnosti Země (M) a vzdálenosti tělesa od jejího těžiště (r).
Budoucnost patří aluminiu.
Offline
#8 21. 08. 2016 14:08
Re: Gravitace a padajici telesa.
Dobře, popíšu jak nad tím přemýšlím.
Pustím z výšky na Zem kuličku z olova a změřím čas dopadu. Pak to samé udělám se stejně velkou kuličkou a ze stejně velké výšky, ale tentokrát kulička bude vážit stejně jako Jupiter.
Za jak dlouho dopadne? Teď už je patrné, že gravitační zrychlení, které udává kulička Zemi nemůžu zanedbat.
Je totiž asi 2 x větší než gravitační zrychlení samotné Země, na kterou kuličku pouštím. Je tedy jasné, že čas dopadu bude podstatně kratší, než v předešlém případě.
A to z toho důvodu, že kromě toho, že Země přitahuje kuličku zrychlením 9,8 g, přitahuje kulička Zem zrychlením cca 23 g. Dohromady se tedy k sobě přibližují zrychlením 32,8g.
Což bezesporu způsobí podstatně hratší čas dopadu (srážky).
V praxi je jediný rozdíl v tom, že asi nikdy nebudeme házet tak těžký předmět, aby to bylo vůbec možné rozdíl v čase dopadu změřit. Mimo jiné by dopad takové kuličky Zemi asi úplně neprospěl a byl by to pravděpodobně poslední pokus, který lidstvo provedlo.
Offline
#9 21. 08. 2016 19:10
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Gravitace a padajici telesa.
↑ pavoda:
ale když "přemýšlíš", tak bys měl opravdu aspoň trochu přemýšlet. Jestliže se ptáš, které těleso "dopadne na Zem", říkáš tím právě to, že hmotnost obou těles lze vzhledem ke hmotnosti Země zanedbat. Jestliže totiž bude mít kulička hmotnost Jupiteru, pak nebude padat kulička na Zemi, ale Země na kuličku...
Budoucnost patří aluminiu.
Offline
#10 21. 08. 2016 19:35
Re: Gravitace a padajici telesa.
↑ Eratosthenes:
Já tvrdím, že těžší těleso dopadne na Zemi za kratší čas. A je úplně jedno, jestli tomu chceš říkat, že spadne kulička na zem nebo Zem na kuličku. Je to asi jako kdyby jsi chtěl vědět za jak dlouho dojede auto cyklistu, přitom by jsi rychlost jízdy cyklisty jednoduše zanedbal.
A je velmi zajímavé sledovat ty vaše povýšenecké reakce pánové.
Offline
#12 24. 08. 2016 02:06
Re: Gravitace a padajici telesa.
Ehm, obmedzme sa na padajuce hmotne body (dovod: za aky cas dopadne gula s polomerom 1 meter na zem z vysky 1 meter?).
Potom dokonca vseobecna relativita postuluje, ze kazde teleso bude padat rovnako a teda dopadne za rovnaky cas, bez ohladu na jeho hmotnost - tzv. princip ekvivalencie.
pavoda napsal(a):
Teď už je patrné, že gravitační zrychlení, které udává kulička Zemi nemůžu zanedbat.
Pracujme v taziskovej sustave Zeme - volba taziskovej sustavy nemoze ovplyvnit vysledok (tu uz bez relativity). Checkm8.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Gravitace a padajici telesa. (TOTO TÉMA JE VYŘEŠENÉ)
