Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2016 19:31
Důkaz - odmocniny
Ahoj, mám tady dvě typově podobné úlohy, se kterými si nevím rady.
Dokažte, že platí následující rovnost:
a) 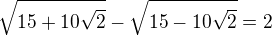
b) 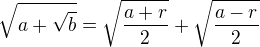 kde
kde 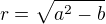
Jde mi o ten princip, jak mám postupovat, když je pod odmocninou další odmocnina? U toho druhého příkladu jsem tam zkoušela za r dosadit, ale přijde mi, že se to ještě více zkomplikovalo. Děkuji za rady.
Offline
#2 28. 08. 2016 09:57 — Editoval misaH (28. 08. 2016 09:58)
- misaH
- Příspěvky: 13460
Re: Důkaz - odmocniny
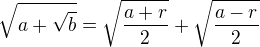
Pýtame sa, či je to pravda, nad = musí byť otáznik.
Umocniť obidve strany: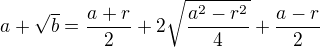
Nad = treba dať otáznik.
Dosadiť za 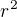 a tak ďalej.
a tak ďalej.
Analogicky prvý príklad. Nezabudnúť na otáznik nad rovná sa.
Offline
#3 28. 08. 2016 10:22 — Editoval vanok (28. 08. 2016 10:53)
Re: Důkaz - odmocniny
Ahoj ↑ Olínečka:,
To prve nemoze ti nic dat, lebo v skutocnosti 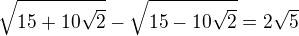
Inac ak ide o pravdive rovnosti, tak jedna ( trikova metoda )je vynasobit prvu rovnost konjugovanym vyrazom. ( tu To by bolo 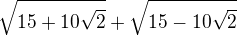 a vyuzit potom identitu "rozdiel stvorcov". Potom polozit
a vyuzit potom identitu "rozdiel stvorcov". Potom polozit 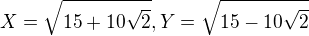 a nakoniec vyriesit system X+Y=...,X-Y=...
a nakoniec vyriesit system X+Y=...,X-Y=...
Ktoreho riesenie umozni ukoncit dokaz.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 28. 08. 2016 10:29 — Editoval vanok (28. 08. 2016 10:31)
Re: Důkaz - odmocniny
Poznamka.
Pochopitelne aj metoda od↑ misaH: (pozdravujem ) funguje, i ked je trosku dlhsia.
Ale tak ci tak pozor na prvu otazku. Treba ju napisat najprv bez chyby.
Druhu som neoveroval.... Ale aj metoda co som popisal funguje.
Kde si nasla toto pekne cvicenie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 29. 08. 2016 10:30 — Editoval Rumburak (29. 08. 2016 10:46)
Re: Důkaz - odmocniny
↑ Olínečka:
Ahoj. Zdravím i ostatní účastníky diskuse.
Poznamenejme, že umocnění rovnosti "na druhou" není ekvivelentní úprava, neboť například
 ,
,
přestože 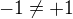 .
.
S implikací  samozřejmě žádný problém není, avšak obrácená mplikace
samozřejmě žádný problém není, avšak obrácená mplikace
(1) 
v oboru reálných čísel je platná pouze tehdy, když čísla 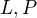 mají stejná znaménka nebo když alespoň
mají stejná znaménka nebo když alespoň
jedno z nich je 0.
U dokazované rovnosti 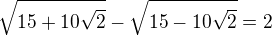 je zřejmé, že její pravá strana je kladná.
je zřejmé, že její pravá strana je kladná.
Chtělo by ještě ověřit, že i levá strana je alespoň nezáporná. Teprve pak bude použití impikace (1) korektní.
Offline
#7 29. 08. 2016 12:45
Re: Důkaz - odmocniny
Pozdravujem ↑ Rumburak:,
Pozor
Tu som ↑ vanok: upozornil na chybu v texte cvicenia. A tak mozes overit ze 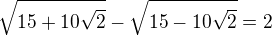 je chybne....
je chybne....
Po overeni som dostal 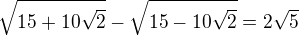
Ubohy stredoskolaci! To asi neuvidia bez pomoci.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 29. 08. 2016 15:00
Re: Důkaz - odmocniny
Ahoj ↑ Cheop:,
Ano aj to pekna metoda. Variacie na tu temu su bohate.
Jedina tazkost, podla mna, bola nast tu chybu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 29. 08. 2016 16:02
Re: Důkaz - odmocniny
↑ Rumburak:
Ano to mozme dufat, ze stredoskolaci co robia take cvicenia, vedia o tom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 29. 08. 2016 17:56 — Editoval vanok (29. 08. 2016 17:57)
Re: Důkaz - odmocniny
Pozdravujem ↑ zdenek1:,
Mas uplne pravdu.
A takato varianta by mozno sa mohla pridat do festivalu fantazii.
Napisem len zaciatok.![kopírovat do textarea $\sqrt{15+10\sqrt{2}}-\sqrt{15-10\sqrt{2}}=
\sqrt 5\[\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\]=...$](/mathtex/60/60070d1c47982b9c472e3b1087032d53.gif)
( prazdniny este vsade neskoncili 😀)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline