Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 04. 2009 20:10
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
derivace
potreboval bych stimhle prikladem pomoc
.png)
.png)
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#3 29. 04. 2009 20:25 — Editoval PitBull~--! (29. 04. 2009 20:27)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: derivace
aby  tak x muze tovnat 0?
tak x muze tovnat 0?
a (2/3)'=0 nebo =2/3 ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#4 29. 04. 2009 20:38
Re: derivace
↑ PitBull~--!:
(2/3)'=0 ale jen jako absolutní člen, (2/3x)'=2/3
R. P. Feynman:Fyzika je jako sex, může přinést praktické výsledky, ale to není důvod, proč to děláme.
Offline
#5 29. 04. 2009 21:03
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: derivace
.png)
jak vypocitam y' a y''?
znam zpusob ale u tohoto prikladu mi dela problem.
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#7 29. 04. 2009 21:47
Re: derivace
↑ PitBull~--!:
Tak jde o vzorec, který ti tu psal halogan (y' - první derivace; y'' - druhá derivace, tj. zderivuješ první derivaci).
↑ M@rvin:
Pokud používáš v exponentu/indexu více, jak jeden psaný znak, pak argument uzavři do složených závorek (svorky {}).
Tvůj texový zápis by pak měl vypadat takto:
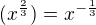
Offline
#9 29. 04. 2009 21:54 — Editoval PitBull~--! (29. 04. 2009 21:55)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: derivace
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#11 29. 04. 2009 22:35 — Editoval PitBull~--! (29. 04. 2009 22:36)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: derivace
.png) ?
?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline


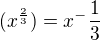
.png)
.png) ?
?