Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 09. 2016 21:13
metrika
zdravím
potreboval by som pomoc s dôkazom.
mám množinu  všetkých postupností reálnych čísel a funkciu
všetkých postupností reálnych čísel a funkciu  , kde
, kde  , podobne pre
, podobne pre  .
.
potrebujem dokázať trojuholníkovú nerovnosť, teda ak  , tak
, tak 
moja myšlienka bola odhadovať člen 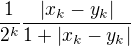 zhora, no nepohol som sa (neviem ako )
zhora, no nepohol som sa (neviem ako )
za každú pomoc ďakujem.
Per aspera ad astra
Offline
#2 26. 09. 2016 22:44 — Editoval vanok (26. 09. 2016 22:45)
Re: metrika
Ahoj,
Ukaz najprv, ze
Ak d(x,y ) je distance na R tak aj  je tiez distance na R.
je tiez distance na R.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 27. 09. 2016 19:07
Re: metrika
↑ vanok:
podobne, prvé dve vlastnosti metriky sú jasné, no s treťou je problém
zobral som to z tejto strany 
lenže keď by som použil tú istú vlastnosť aj v menovateli , tak by som dostal opačnú nerovnosť, akú potrebujem a nič iné mi nenapadá.
Per aspera ad astra
Offline
#4 27. 09. 2016 22:32 — Editoval vanok (28. 09. 2016 10:08)
Re: metrika
Najlepsie je asi pouzit znamu vlasnost
Nech (X,d) je metricky priestor a nech  stupajuca ( croissante) sous-additivna a nulova len v 0:
stupajuca ( croissante) sous-additivna a nulova len v 0:
a 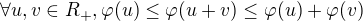
Potom  je tiez distance na X.
je tiez distance na X.
Toto iste vies dokazat.
No ale aj priamy dokaz tvojej vlasnosti je mozny, a pochopitelne sa mozes inspirovat predoslou vladnostou.
Édit. Co mozes konstatovat o 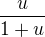 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 28. 09. 2016 09:28
#6 28. 09. 2016 14:34 — Editoval vanok (29. 09. 2016 06:58)
Re: metrika
Ahoj,
Priidam ti trochu podrobnejsi navod. ... ide opriamy dokaz ale niektore uvahy z neho ti umoznia dokazat aj vlastnost co som napisal vyssie.
Lahko ukazes ze  taka ze
taka ze  je rastuca ( croissante) na
je rastuca ( croissante) na 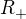
(Vdaka variacii f, lebo f'= ???? a  )
)
Co da  ?
?
Poloz 
Over axiomy metriky pre d'
Co sa tyka tretiej axiome, vyuzi, ze  ako aj podobnu relaciu pre
ako aj podobnu relaciu pre 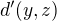 a tiez pouzi, ze
a tiez pouzi, ze 
(Napis preco platia tie nerovnosti)
Napis nam tu uplne cely dokaz, takto budeme isty ze ho vies dokonale urobit.
A potom mozes lahko doriesit tvoj povodny problem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
