Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 05. 2009 16:16
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
prubeh funkce
prosim pomocte mi nekdo vyresit tenhle priklad y=sinx+cosx
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#3 01. 05. 2009 17:31
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
napsal sem jenom tohle ani nevim jestli je to dobre nebo ne co tye goniometrie tak sem strasne blbej
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#4 01. 05. 2009 17:33
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: prubeh funkce
Zatím to vypadá dobře. Najdi ještě průsečíky s osami a pokračuj v extrémech.
Pracuj zatím jen na intervalu <0; 2pi>, ta funkce totiž bude mít periodu 2pí, takže stačí jen tento interval.
Offline
#5 01. 05. 2009 17:44
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
no to je prave ten problem...
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#6 01. 05. 2009 17:58
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: prubeh funkce
Tak průsečíky:
dosaď za x nulu a získáš průsečík s y. Pak tam dosaď 2 pí a dostaneš funkční hodnotu ve 2 pí (ani nemusíš, je stejná jako v nule :))
pak řeš rovnici 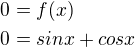
Buď přes tvé oblíbené součtové vzorce, nebo přes jednotkovou kružnici.
Teď máš průsečíky, extrémy, monotónost je asi jasná.
Offline
#7 01. 05. 2009 18:59
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
jak vyresim rovnice sinx+cosx=0 ? ja umim jenom sinx-cosx=0 protoze sem na to mel napovedu
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#8 01. 05. 2009 19:23
Re: prubeh funkce
Existuje hodně možností, jak tuto rovnici vyřešit :-) Velmi hrubou možností, která asi napadne většinu středoškoláků, je upravit 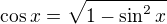 (či totéž pro sinus), což sice k cíli vede, ovšem jsou nutné nějaké zkoušky a diskuse.
(či totéž pro sinus), což sice k cíli vede, ovšem jsou nutné nějaké zkoušky a diskuse.
Ukážu proto pár (dle mého názoru) elegantních řešení:
1)
Umocníme:
s čímž už si snadno poradíme (přinejhorším substituce za 2x).
2)
Upravujeme:
Nyní si už můžeme vybrat, jestli budeme řešit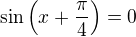
nebo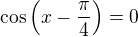
3)
Úplně nejdrsnější :-) Substituujeme 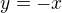
Pak řešíme rovnici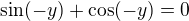
což pomocí parity goniometrických funkcí můžeme upravit na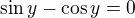
což je rovnice, kterou už dle tvého vyjádření řešit umíš :-)
Offline
#9 01. 05. 2009 19:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: prubeh funkce
↑ Olin:
Zdravím,
nám v Zahrádkach řikali, že stačí umět jednotkovou kružnici a vědet, pro kterou hodnotu úhlu maji sinx a cos x stejnou (pro pripad sin x - cos x =0) nebo opačnou hodnotu - pro případ, který řešite.
Offline
#10 01. 05. 2009 19:52
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
aha tak to ja sem zase resil tak ze dam misto sinx=cos(pi/2-x) nebo naopak
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#11 01. 05. 2009 20:20
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
jak zjistim monotonost u y' a y''a jak nakreslim tabulku ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#12 01. 05. 2009 20:20
Re: prubeh funkce
↑ jelena:
Jasně, jenže lidé si většinou pamatují jen ty body, kde mají stejnou hodnotu. Samozřejmě se dá snadnou úvahou odvodit, kde budou ty body, kde mají hodnotu opačnou.
Ještě mě teď kolega upozornil, že takové "správné středoškolské" řešení je dělit kosinem, čímž dostaneme rovnici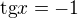 .
.
Offline
#13 01. 05. 2009 20:22
Re: prubeh funkce
↑ PitBull~--!:
Co přesně potřebuješ zjistit? Monotónnost první a druhé derivace, kde y je co? Nějaká obecná funkce?
A jakou tabulku?
Offline
#14 01. 05. 2009 21:36
- marnes

- Příspěvky: 11227
Re: prubeh funkce
↑ PitBull~--!:
Jen další možnost
sinx+cosx=0 /Odm(2) obecně odm(a^2+b^2) kde a a b vyčteme z rovnice asinx+bcosx=0
sinx/odm(2)+cosxodm(2)=0
odm(2)/2. sinx + odm(2)/2.cosx=0 a podle součtového vzorce sin(x+y)=...
sin(x+pí/4)=0 a tato rovnice už je jednoduchá a nemusí být zkouška
Jo. A na začátku vás zdravím.
Offline
#15 01. 05. 2009 21:39 — Editoval PitBull~--! (01. 05. 2009 22:10)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
↑ Olin:
tabulku na extremni (max,min) , konkavnost a inflexni bod
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#16 01. 05. 2009 21:43 — Editoval PitBull~--! (01. 05. 2009 21:48)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: prubeh funkce
↑ marnes:
a jak zjistim v jake bode je grav maximum a v jake bode je minimum a u y'' zase konkav. konvex. ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#17 01. 05. 2009 23:42 — Editoval O.o (02. 05. 2009 11:32)
Re: prubeh funkce
↑ PitBull~--!:
Ahoj -),
myslím, že ti pomůže jedno tlačítko Hledat a parametr Průběh funkce.
Offline
#18 02. 05. 2009 10:38
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: prubeh funkce
↑ O.o:Nemá cenu dávat odkazy tohoto typu.
Zkus spíš
Code:
http://forum.matweb.cz/search.php?action=search&keywords=KLÍČOVÉ_SLOVO&author=AUTOR_PŘÍSPĚVKU&show_as=topics
V našem případě
http://forum.matweb.cz/search.php?actio … _as=topics
BRKOS - matematický korespondenční seminář pro střední školy
Offline