Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 10. 2016 16:17
Půlkružnice nad průměry
Je dána úsečka AB = a se středem S. Nad průměry AB, AS, BS jsou sestrojeny půlkružnice tak, že leží v téže polorovině s hranicí AB.
Vypočítejte poloměr r kružnice, která se dotýká všech tří půlkružnic.
Poradil by prosím někdo postup?
Offline
- (téma jako vyřešené označil(a) xx)
#4 23. 10. 2016 16:47
#6 23. 10. 2016 16:53 — Editoval misaH (23. 10. 2016 16:55)
- misaH
- Příspěvky: 13460
Re: Půlkružnice nad průměry
Keď je polomer veľkej kružnice  a hľadaná dĺžka
a hľadaná dĺžka 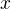 , tak
, tak
Alebo nie?
Offline
#12 23. 10. 2016 17:35 — Editoval Al1 (23. 10. 2016 17:36)
Re: Půlkružnice nad průměry
Nehledej myšlenkové pochody kolegyně misaH. Zaměř se na své řešení. :-)
Offline




 , x je hledaný poloměr, tedy
, x je hledaný poloměr, tedy 
