Matematické Fórum

misicka5465 · 25. 10. 2016 16:43

Ahojte,potrebovala by som pomôcť s príkladom :

Nájdite všetky 3 tretie odmocniny z čísla (2 + 3i)∧3

Andrejka3 · 26. 10. 2016 10:41

Ahoj.
Našla jsi aspoň jednu třetí odmocninu?

misicka5465 · 26. 10. 2016 12:51

Andrejka3 · 26. 10. 2016 13:07

↑ misicka5465:
Jo.

Dejme tomu, že další lze dostat tak, že tu tvoji třetí odmocninu přenásobíš nějakým komplexním číslem $z$ .
$z\cdot (2+3i)$

O tom čísle z se něco dozvíš, když vypočítáš třetí mocninu čísla $z\cdot (2+3i)$ .

misicka5465 · 26. 10. 2016 13:23

↑ Andrejka3:
Vyšlo mi
-46z∧3+9iz∧3

Andrejka3 · 26. 10. 2016 13:41

↑ misicka5465:
Ok. Nebylo potřeba roznásobovat. Stačí to takhle:
$\big(z\cdot (2+3i)\big)^3=z^3\cdot(2+3i)^3$ . Tak, a my chceme, aby $z\cdot (2+3i)$ byla třetí odmocnina z $(2+3i)^3$ , tedy aby
$z^3\cdot(2+3i)^3 =(2+3i)^3$ .

Co z poslední rovnice plyne pro $z^3$ ?

misicka5465 · 26. 10. 2016 13:50

↑ Andrejka3:

$z_{ } 3=\frac{(2+3i)^{3}}{(2+3i)^{3}}=1$

Andrejka3 · 26. 10. 2016 13:54

↑ misicka5465:
Neboli $z$ je třetí odmocnina z jedné. Ty jsou celkem tři. Umíš je najít?
Až je budeš mít, dostaneš tak i tři různé třetí odmocniny z $(2+3i)^3$

misicka5465 · 26. 10. 2016 14:14

↑ Andrejka3:
z=1
z= $(-1i)^{2}$
z= $i^{4}$

? Som z toho už trocha popletená

Andrejka3 · 26. 10. 2016 14:37

↑ misicka5465:
To je jednička, třikrát jinak. Máš zatím jen jednu třetí odmocninu z jedné.

Hodí se znát goniometrický tvar cpx čísla a Moivre-ovu větu. Co se děje s velikostí cpx čísla při umocňování a co s argumentem.

misicka5465 · 26. 10. 2016 14:51

z=1
z=-0,5+0,866i
z=-0,5-0,866i

??↑ Andrejka3:

Andrejka3 · 26. 10. 2016 14:59

↑ misicka5465:
Myslím, že to máš dobře. Teď teda máme: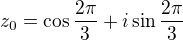
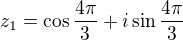$z_0=\cos \frac{2\pi}{3}+i\sin\frac{2\pi}{3}$ ,
$z_1=\cos \frac{4\pi}{3}+i\sin\frac{4\pi}{3}$ a
$z_2=1$ .
Řešení původního problému je
$(2+3i)\cdot z_0$ ,
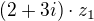$(2+3i)\cdot z_1$ a
$(2+3i)\cdot z_2$ .

misicka5465 · 26. 10. 2016 15:01

↑ Andrejka3:
Ďakujem veľmi pekne za pomoc.Veľmi mi to pomohlo.

Andrejka3 · 26. 10. 2016 15:02

↑ misicka5465:
Rádo se stalo. Ve svém úvodním příspěvku máš vpravo dole možnost téma označit jako vyřešené.
Měj se.

Matematické Fórum

#1 25. 10. 2016 16:43

3.odmocnica z komplexného čísla

#2 26. 10. 2016 10:41

Re: 3.odmocnica z komplexného čísla

#3 26. 10. 2016 12:51

Re: 3.odmocnica z komplexného čísla

#4 26. 10. 2016 13:07

Re: 3.odmocnica z komplexného čísla

#5 26. 10. 2016 13:23

Re: 3.odmocnica z komplexného čísla

#6 26. 10. 2016 13:41

Re: 3.odmocnica z komplexného čísla

#7 26. 10. 2016 13:50

Re: 3.odmocnica z komplexného čísla

#8 26. 10. 2016 13:54

Re: 3.odmocnica z komplexného čísla

#9 26. 10. 2016 14:14

Re: 3.odmocnica z komplexného čísla

#10 26. 10. 2016 14:37

Re: 3.odmocnica z komplexného čísla

#11 26. 10. 2016 14:50 Příspěvek uživatele misicka5465 byl skryt uživatelem misicka5465.

#12 26. 10. 2016 14:51

Re: 3.odmocnica z komplexného čísla

#13 26. 10. 2016 14:59

Re: 3.odmocnica z komplexného čísla

#14 26. 10. 2016 15:01

Re: 3.odmocnica z komplexného čísla

#15 26. 10. 2016 15:02

Re: 3.odmocnica z komplexného čísla

Zápatí