Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 10. 2016 15:01 — Editoval Evkaa (26. 10. 2016 15:48)
Matematická indukce
Zdravím, máme vyřešit tohle pomocí matematické indukce, poradil by mi někdo, jak dál postupovat:
Zadání příkladu je: \ge
\ge 
Tak první krok je, že za n si dosadím 1, takže mi po úpravě výjde:


V dalším kroku udělám n=k:
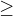

V dalším kroku udělám n=k+1:
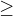

Když si to poupravím, výjde mi:
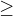

Můžu se zeptat, jak tedy postupovat dál?
Offline
#2 26. 10. 2016 15:15
Re: Matematická indukce
Ahoj ↑ Evkaa:,
Tvoj zaciatok nie je uz pravdivy.
Vsak toto  neplati.
neplati.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 26. 10. 2016 17:35 Příspěvek uživatele Al1 byl skryt uživatelem Al1. Důvod: nechám radit kolegy :-)
#6 26. 10. 2016 19:22
- Kristynaaa

- Příspěvky: 50
- Škola: "MFF"
- Pozice: Student
- Reputace: 0
Re: Matematická indukce
Ja vim. Jen proste mi nebylo nejak extra odpovezenk a neumim s tim hnout.
Offline
#7 26. 10. 2016 20:11 — Editoval vanok (26. 10. 2016 21:35)
Re: Matematická indukce
↑ Evkaa:
Po oprave je to lepsie, ale treba napisat lepsie tvoju structuru dokazu. A doplnit to najdolezitejsie, co je dokaz v indukcnom kroku.
Tak to by som pisal napr. takto
Chceme dokazat matematickou indukciou, ze  (P(n)). pre vsetki
(P(n)). pre vsetki  ( prepokladame ako je zvykom v Cesku ze nula nie je prirodzene cislo).
( prepokladame ako je zvykom v Cesku ze nula nie je prirodzene cislo).
Dokaz.
Iniciacia.
Preto je treba overit  co sa pise:
co sa pise: hned vidime ze plati.
hned vidime ze plati.
Indukcny krok. Co znamena, predpoklame  , cize
, cize
a vdaka tomu dokazeme  co sa pise
co sa pise 
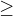

Ked vynasobime obe strany  z
z 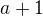 dostaneme
dostaneme
doteraz som opravil tvoje nezrozumitelne pokusy na zrozumitelny text. ( poriadne to prestuduj)
Teraz treba skusit nieco najst aby z posledneho vzorca si dostala  . Co ukonci tvoj dokaz.... hladaj trochu.
. Co ukonci tvoj dokaz.... hladaj trochu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 ze.
ze.