Matematické Fórum

Feek · 12. 11. 2016 16:59 — Editoval Feek (12. 11. 2016 17:00)

Ahoj, neporadil by mi někdo, proč má následující rovnice kořen i v nule? Pokud levou stranu upravím, dostanu sice kladné exponenty, ovšem původní výraz na LS není v nule definován - nemělo by být řešení jen jedno - nenulové? Mám v tom zmatek.

$\frac{(2-\frac{4}{x})}{(1-\frac{2,7}{x}+\frac{0,9}{x^2})}=0$

Kořeny pomocí Wolframu jsou následující:

$x=0$
$x=2$

Děkuji.

Eratosthenes · 12. 11. 2016 17:08

ahoj ↑ Feek:,

samozřejmě - zlomek je roven nule právě tehdy, je-li nulový čitatel a nenulový jmenovatel, tj. 2-4/x =0, takže x=2´. Nula je nesmysl, protože v ní rovnice není definována.

vanok · 12. 11. 2016 17:12

Ahoj ↑ Feek:,
Ked sa zbavis zlomkov v rovnici... dostanes rovnicu ktora ma riesenie aj x=0.
No v povodnej x=0, nie je mozne, lebo by islo o delenie nulov... co je nemozne.

Preto ak sa pouzije implikacia pri rieseni rovnice skuska v povodnej rovnica je povinna.... lebo implikacia moze pridat riesenia co nevyhovuju povodnej rovnicu.

Feek · 12. 11. 2016 17:20

Děkuji, zarazilo mne to... Je nějaký důvod, proč výpočetní programy berou v tomto případě jako kořen i tu nulu viz Wolfram nebo i Matlab?

jelena · 12. 11. 2016 23:35

Zdravím,

přesunu to do sekce CAS, zda někdo z kolegů nebude mít upřesnění. WA provádí úpravu (viz Alternate form) a při ručně takové úpravě bychom museli vykratit x (tedy by byla podmínka 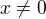$x\neq 0$ , nebo bychom tuto podmínku napsali již na úvod řešení). Kolegům děkuji za upřesnění.

vanok · 24. 11. 2016 09:38

Pozdravujem ↑ jelena:,
Pri rieseni rovnic sa casto pracuje z implikaciamy.
Co neznamena ze povodna rovnica a upravena rovnica maju identicke riesenia ( vdaka vlasnostiam implikacie uprave rovnica ma viacej rieseni ako povodna)
Preto skuska je nevyhnutna cast hladania rieseni.

Je celkom mozne, ze v formalnych vypoctoch sa daju este robit pokroky. ...

jarrro · 24. 11. 2016 10:46 — Editoval jarrro (24. 11. 2016 10:47)

Wolframalpha "zabŕda" do komplexnej analýzy aj tam kde nemusí teda čo nie je definované "predpisom" berie ako analytické pokračovanie. Limita v nule je (aj v reálnej analýze) nulová preto to zobral ako riešenie (aspoň si myslím)

kaja.marik · 27. 11. 2016 08:51

Feek napsal(a):
Děkuji, zarazilo mne to... Je nějaký důvod, proč výpočetní programy berou v tomto případě jako kořen i tu nulu viz Wolfram nebo i Matlab?

Ty vypocetni programy jsou jinak chytre nez lidi a zatimco lidi vidi na prvni pohled ze nula nevyhovuje, algoritmu to byt jasne nemusi. Resi se napriklad zde: https://trac.sagemath.org/ticket/2617#comment:16

kaja.marik · 27. 11. 2016 08:54

↑ jarrro:
Dalsi mozne vysvetleni je, ze aby se dala rovnice predhodit algoritmu pro reseni rovnic, musi se upravit do nejakeho kanonickeho tvaru. A to bude v tomto pripade asi ten, kde je uz mozne mit i x=0, protoze se upravi slozeny zlomek.

Feek · 30. 11. 2016 18:41

Dobře, děkuji.

Matematické Fórum

#1 12. 11. 2016 16:59 — Editoval Feek (12. 11. 2016 17:00)

Kořeny rovnice

#2 12. 11. 2016 17:08

Re: Kořeny rovnice

#3 12. 11. 2016 17:12

Re: Kořeny rovnice

#4 12. 11. 2016 17:20

Re: Kořeny rovnice

#5 12. 11. 2016 23:35

Re: Kořeny rovnice

#6 24. 11. 2016 09:38

Re: Kořeny rovnice

#7 24. 11. 2016 10:46 — Editoval jarrro (24. 11. 2016 10:47)

Re: Kořeny rovnice

#8 27. 11. 2016 08:51

Re: Kořeny rovnice

Feek napsal(a):

#9 27. 11. 2016 08:54

Re: Kořeny rovnice

#10 30. 11. 2016 18:41

Re: Kořeny rovnice

Zápatí