Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 09. 2016 20:24
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
P.K. Teorémy
Zdravím. Dovolím si představit výběr poznatků ze svého osobního bádání. Pokusíte se nalézt důkazy?
Teorém č.1

P.K.
Offline
#2 11. 11. 2016 16:24 — Editoval PlusPlusPlus (15. 11. 2016 20:45)
#3 12. 11. 2016 11:16
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
Teorém č.3 - naleznete důkaz ?
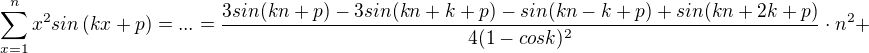


P.K.
Offline
#4 12. 11. 2016 22:46
Re: P.K. Teorémy
↑ PlusPlusPlus:
Jednoduše se ukáže, že![kopírovat do textarea $
\sum_{k=1}^p&\sin\left(\cos\left(xk-\frac{x}{2}\right) \right)\cdot\cos\left(\sin\left(xk-\frac{x}{2}\right)\cdot\cot\left(\frac{x}{2}\right)\right)\\[.5\baselineskip]
&=\sum_{k=1}^p\sin\left(\frac{\sin kx-\sin((k-1)x)}{2\sin\frac x2}\right)\cdot\cos\left(\frac{\sin kx+\sin((k-1)x)}{2\sin\frac x2}\right)\\[.5\baselineskip]
&=\frac 12\sum_{k=1}^p\left(\sin\left(\frac{\sin kx}{\sin\frac x2}\right)-\sin\left(\frac{\sin((k-1)x)}{\sin\frac x2}\right)\right)\\[.5\baselineskip]
&=\frac 12\sin\left(\frac{\sin px}{\sin\frac x2}\right)
$](/mathtex/a7/a79dc27317d17d2ef1dd60ba40775cb7.gif)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 12. 11. 2016 23:14
Re: P.K. Teorémy
↑ PlusPlusPlus:
Stačí ukázat, že platí rovnost
Jednoduše se ukáže, že
Na druhou stranu
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 13. 11. 2016 11:24
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
↑↑ Pavel:
Děkuji za reakci a Váš čas. Přes dva sousední členy, to mě při konstrukci příkladu nenapadlo. OK - velmi lehké.
Offline
#7 13. 11. 2016 19:01 — Editoval PlusPlusPlus (15. 11. 2016 20:44)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
Teorém č.4 - kubicko - geometrická řada, naleznete důkaz ?
Důkaz existuje
Offline
#8 13. 11. 2016 20:28 — Editoval PlusPlusPlus (16. 11. 2016 19:18)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
Teorém č.5 - motivační
Nalezení obecného vzorce pro rozklad mnohočlenu  na součin pro sudé
na součin pro sudé  .
.
Důkaz existuje
Offline
#9 13. 11. 2016 21:03
Re: P.K. Teorémy
Zdravím ↑ PlusPlusPlus:,
to rozhodně není nic nového, protože lze snadno nahlédnout, že známý vzorec platí i pro komplexní čísla. Váš vzorec je pouze speciální případ tohoto.
platí i pro komplexní čísla. Váš vzorec je pouze speciální případ tohoto.
Offline
#10 13. 11. 2016 21:26 — Editoval Pavel (13. 11. 2016 21:28)
Re: P.K. Teorémy
↑ PlusPlusPlus:
koeficient  se zdá být nadbytečný. Jinými slovy, vzorec by bylo možné zjednodušit nahrazením výrazu
se zdá být nadbytečný. Jinými slovy, vzorec by bylo možné zjednodušit nahrazením výrazu 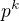 např. proměnnou
např. proměnnou  . Nic se ve významu vzorce nezmění.
. Nic se ve významu vzorce nezmění.
Důkaz kubicko-geometrické řady lze provést několika způsoby - řešením speciální diferenční rovnice, vhodným derivováním a integrováním jisté mocninné řady, elementárními úpravami z teorie diferenčního a sumačního počtu využívající Abelovy parciální sumace apod.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 15. 11. 2016 19:54
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
↑↑ Bati:,
Jsem již starší člověk, takže mě některé věci trvají déle, než je pochopím. Z Vašeho příspěvku vidím, že Vámi uvedený vzorec rozkládá dvojčlen na součin, po dosazení  je však výsledkem rozdíl dvojčlenu
je však výsledkem rozdíl dvojčlenu  , nikoliv jeho součet
, nikoliv jeho součet 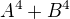 .
.
Můžete mě tedy napsat rozklad  a
a  , případně obecný vzorec pro libovolný součet dvojčlenu se sudým exponentem?
, případně obecný vzorec pro libovolný součet dvojčlenu se sudým exponentem?
Mě se podařilo dohledat například tyto rozklady: http://www.aristoteles.cz/matematika/mo … oclenu.php Téma o kterém jsem psal, jsem na internetu, ani v mých zakoupených knihách nedohledal.
Děkuji za Váš čas.
Offline
#12 15. 11. 2016 20:34
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
Zdravím ↑↑ Pavel:
Jasně, lze napsat  , a obsah závorky brát jako nějaký qocient geometrické řady.
, a obsah závorky brát jako nějaký qocient geometrické řady.
Je možné Vámi uvedenými způsoby odvozovat i součty řad 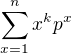 s vyššími přirozenými exponenty
s vyššími přirozenými exponenty  ? Mě se v oblasti řad podařilo dospět k mnoha užitečným poznatkům, které rád v budoucnu zveřejním.
? Mě se v oblasti řad podařilo dospět k mnoha užitečným poznatkům, které rád v budoucnu zveřejním.
Zbývá pouze řada  , řešení výpočtu je obecně známé ???
, řešení výpočtu je obecně známé ???
Offline
#13 15. 11. 2016 21:04
#14 16. 11. 2016 19:11 — Editoval PlusPlusPlus (16. 11. 2016 21:32)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: P.K. Teorémy
Ahoj ↑↑ Bati:,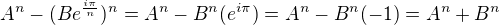
Tak to se mě stává opravdu často. Zapomínám, nebo přehlížím. Děkuji za Váš příspěvek. Pro Vás maličkost, pro mě přínosná hodnota.
Zmátla mě skutečnost, že se v mém postupu a následném odvození nevyskutuje 
Offline

![kopírovat do textarea $ (k,p\in\mathbb{R})\wedge (p^k\neq \mathrm 1) \wedge [\forall (p>0) \vee \exists (p<0)]$](/mathtex/94/94bcd9680e131255a6602011f426be37.gif)
![kopírovat do textarea $\sum_{x=1}^nx^3 p^{kx} = . . . =p^{kn+k} \left[ \frac{n^3}{p^k-1}-\frac{3n^2}{(p^k-1)^2} +\frac{(3+3p^k)n}{(p^k-1)^3} -\frac{4p^k+p^{2k}+1}{(p^k-1)^4} \right]+p^{k} \left[ \frac{4p^k+p^{2k}+1}{(p^k-1)^4} \right]$](/mathtex/96/962b6d608d504bcbe4ee73d9a53bd638.gif)
 , respektive z řady pro součet jejich prvních n-členů
, respektive z řady pro součet jejich prvních n-členů 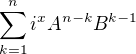 . Protože z níže uvedené ukázky jsou zřejmé exponenty
. Protože z níže uvedené ukázky jsou zřejmé exponenty 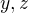 , schází pouze správně vyjádřit exponent
, schází pouze správně vyjádřit exponent  u imaginárního čísla
u imaginárního čísla  .
.

 . Pak
. Pak  .
.