Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 06. 2015 17:08
Exponenciální rovnice
Dobrý den, nemůžu vyřešit dva příklady z Petákové, řešení jsem našla, ale úplně mu nerozumím, jestli někdo napíše podrobné řešení, budu vděčná.
1. 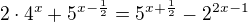
tady jsem se dostala k 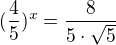 a dál nevím..
a dál nevím..
2. 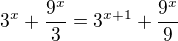
tady mi vyšel nesmysl, 3x-1=3x-1.
Budu moc ráda za pomoc, jenom prosím podrobněji rozepsat, ať pochopím ve kterém kroku mám chybu.
Děkuji!
Offline
- (téma jako vyřešené označil(a) gadgetka)
#2 20. 06. 2015 17:17
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Exponenciální rovnice
Ahoj ↑ Kendy:
Ten první zatím počítám, ale u toho druhého stačí použít substituci 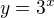 . To umíš ne? :)
. To umíš ne? :)
Offline
#4 20. 06. 2015 17:31 — Editoval xstudentíkx (20. 06. 2015 17:40)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Exponenciální rovnice
↑ Kendy:
Vyšlo mi něco jiného: 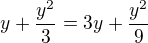 , vypadly ti nejspíš mocniny.
, vypadly ti nejspíš mocniny.
Jinak ten druhý máš do tohoto kroku správně a nyní stačí udělat už jen konečnou úpravu: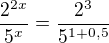 z toho dostaneš:
z toho dostaneš: 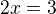 což je to samé jako
což je to samé jako 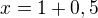 , tudíž výsledek je 1,5 (3/2)
, tudíž výsledek je 1,5 (3/2)
Offline
#7 12. 11. 2016 23:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Exponenciální rovnice
↑ Zdur:
Zdravím, pro nový dotaz si, prosím, zakládej nové téma viz pravidla. K dotazu - vyjádřit ve tvaru y=... to nepůjde, pokud potřebuješ jen výsledek, tak např. WA (nebo bys musel používat některou numerickou metodu). Pokud nepomůže, založ si, prosím, nové téma. Děkuji.
Offline
