Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 15. 11. 2016 21:53

126Magdaléna126
Příspěvky: 30
Reputace:   0 
 

Goniometrické nerovnice

Ahoj, môžem poprosiť o pomoc? ..neviem si dať rady s týmto prikladom,skúšala som to počítať, ale neviem či na to idem dobre..

2$2^{x}-5*4^{×-2}>1-2^{x-1} $

Offline

 

#2 15. 11. 2016 22:03

Al1
Příspěvky: 7782
Reputace:   540 
 

Re: Goniometrické nerovnice

↑ 126Magdaléna126:

Zdravím,

především řešíš exponenciální nerovnici, nikoli goniometrickou.

K řešení: využij 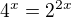$4^{x}=2^{2x}$ a zaveď substituci 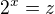$2^{x}=z$ a budeš řešit kvadratickou nerovnici.

Offline

 

#3 15. 11. 2016 22:09 Příspěvek uživatele teolog byl skryt uživatelem teolog.

#4 15. 11. 2016 22:13

126Magdaléna126
Příspěvky: 30
Reputace:   0 
 

Re: Goniometrické nerovnice

↑ Al1:
Viem,źe exponencialne.akurát pozerám,že som tam blbost napísala :/
Spravila som..
Ale vysla mi nejaká krkolomná kvadratická ...
$80y^{2}+2y-1<0$

Môže to byť?..ďakujem zatiaľ

Offline

 

#5 15. 11. 2016 22:43

misaH
Příspěvky: 13459
 

Re: Goniometrické nerovnice

$2^{x}-5*4^{×-2}>1-2^{x-1} $

$0>5\cdot \frac {2^{2x}}{16}-\frac {2^x}{2}-2^x+1$

$0>5\cdot {2^{2x}}-8\cdot {2^x}-16\cdot 2^x+16$

Nie?

Offline

 

#6 15. 11. 2016 22:52

126Magdaléna126
Příspěvky: 30
Reputace:   0 
 

Re: Goniometrické nerovnice

↑ misaH:ďakujem krásne :)

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson