Matematické Fórum

PlusPlusPlus · 11. 11. 2016 22:59

Zdravím všechny příznivce matematiky a matematiky samotné. Toto forum se mě velmi líbí, vždy tu najdu mnoho užitečných informací.
Matematiku mám rád, je to můj nejoblíbenější koníček. Někteří lidé si dopřejí radost tím, že si koupí nejnovější mobil, notebook nebo jinou drahou věc. Mě s přibývajícími lety plně uspokojí zajímavá matematická kniha, mám radost z poznávání. Manželka o mě tvrdí, že jsem divný. Hmm, na každém šprochu, pravdy trochu.

V budoucnu bych rád veřejně publikoval své osobní matematické poznatky. V této souvislosti zakládám na tomto diskusním fóru několik otevřených témat. Do těchto otevřených témat budu postupně přidávat nové příklady a jejich výsledky. Pokusím se zaměřit spíše na kvalitu, než kvantitu. Příklady, které zde vkládám, jsem osobně konstruoval. Nelze je tedy dohledat na jiných diskusích. Některé příklady budou snadné, jiné budou obtížné. Ke všem předkládaným příkladům a jejich výsledkům mám samozřejmě správný postup řešení. Řešení všech příkladů bude zveřejněno v připravované odborné publikaci.

Rád bych Vás požádal o případné příspěvky. Zajímaly by mě Vaše postupy a způsoby řešení příkladů. Pokud Vás příklady neobtěžují a najdete si pár minut na jejich řešení, budu Vám srdečně zavázán.

S pozdravem P.K.

Rozcestník:
http://forum.matweb.cz/viewtopic.php?id=93880

PlusPlusPlus · 11. 11. 2016 23:00

Příklad 1: $\lim_{x \to 3} \frac{x^2-9}{cos(\frac{\pi x^{2}}{18})}= . . . = -\frac{18}{\pi}$ Příklad 2: $\lim_{x \to 2} \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }= . . . = \frac{1}{5}$

PlusPlusPlus

Příklad 3:

$\lim_{n\to\infty } \left[ 2-9\sum_{k=1}^{n}\left( \frac{1}{10} \right)^k \right]^{10^n}= . . . = e$

PlusPlusPlus · 13. 11. 2016 10:19

Příklad 4 - domnívám se, že je již náročnější než předcházející. Možná se pletu:

$\lim_{x\to 5} \left[ 1-\frac{10}{\pi}-\frac{x^2-9x+20}{cos\frac{\pi x}{10}}\right]^{\frac{\pi}{x-5}}= . . . = e^{10}$

PlusPlusPlus

Hoj lidi, nedaří se mě zkontrolovat pomocí nástroje Wolfram některé příklady.

Dříve zkonstruovaný příklad 2, je v pohodě:
$\lim_{x \to 2} \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }= . . . = \frac{1}{5}$ http://www.wolframalpha.com/input/?i=li … +as+x-%3E2

Pokud se ale snažím příklad 2 vytunit, nemůžu si již ověřit správnost výpočtu. Zřejmě je to způsobeno Free licencí Wolframu :
$\lim_{x \to 2} \left[ \frac{4}{5} + \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }\right]^{\frac{50x-20}{(x-2)^2}}= . . . \neq \mathrm e$

Můžete mě prosím výsledek zkontrolovat? Případně pokud mě poradíte jakým způsobem se dá licence Wolframu získat, budu Vám vděčný.
P.K.

mák · 16. 11. 2016 21:59

Zdravím,
Odkaz

PlusPlusPlus

Aha, chybička se vloudila. Je to v tom kosinu. Protože když si to zjednoduším, tak už je vše v pořádku a v souladu s tím, jak jsem konstrukci původně zamýšlel:

$\lim_{x \to 2} \frac{\pi(10x-3x^2-8) }{15\cdot cos(\frac{2\pi x}{3}-\frac{5\pi }{6}) }= . . . = \frac{1}{5}$
http://maxima-online.org/#?inc=r426336821

Po vytunění:
$\lim_{x \to 2} \left[ \frac{4}{5}+ \frac{\pi(10x-3x^2-8) }{15\cdot cos(\frac{2\pi x}{3}-\frac{5\pi }{6}) } \right]^{\frac{10}{3(x-2)}}= . . . = e$
http://maxima-online.org/#?inc=r-72353908

PlusPlusPlus

PlusPlusPlus napsal(a):
Hoj lidi, nedaří se mě zkontrolovat pomocí nástroje Wolfram některé příklady.

Dříve zkonstruovaný příklad 2, je v pohodě:
$\lim_{x \to 2} \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }= . . . = \frac{1}{5}$ http://www.wolframalpha.com/input/?i=li … +as+x-%3E2

Pokud se ale snažím příklad 2 vytunit, nemůžu si již ověřit správnost výpočtu. Zřejmě je to způsobeno Free licencí Wolframu :
$\lim_{x \to 2} \left[ \frac{4}{5} + \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }\right]^{\frac{50x-20}{(x-2)^2}}= . . . \neq \mathrm e$

Můžete mě prosím výsledek zkontrolovat? Případně pokud mě poradíte jakým způsobem se dá licence Wolframu získat, budu Vám vděčný.
P.K.

Aha, uvažoval jsem nesprávně při výpočtu exponentu. Logicky správný výsledek je:
$\lim_{x \to 2} \left[ \frac{4}{5} + \frac{\pi(12x-4x^2-x^3) }{150\cdot cos(\frac{\pi x^{2}}{3}-\frac{4\pi x}{5}+\frac{23\pi }{30}) }\right]^{\frac{54000}{675x^2-2700x+2700+\pi^2(768x-640x^2+64x^3+32x^4)}} = . . . = e$
http://maxima-online.org/#?inc=r1516380521

PlusPlusPlus · 06. 12. 2016 18:30

Dobrý večer,
následující limita konverguje k Eulerovu číslu. Dokázal by někdo z přítomných naznačit postup řešení limity?

$\lim_{x \to\infty } \left( \sqrt{\frac{4x^3+3}{9x^3-x^2} } + \sqrt{\frac{x^2+3x}{9x^2+1} } \right)^{\frac{9}{\sqrt{9+\frac{26}{x} } -\sqrt{9-\frac{1}{x}}+6-\sqrt{36-\frac{4}{x}}}} = . . . = e$

Za reakce děkuji.
P.K.

PlusPlusPlus · 09. 12. 2016 16:44

Dobrý večer,
zkonstruoval jsem následující limitu. Dokázal by někdo naznačit způsob řešení výpočtu? Za reakce děkuji.

$\lim_{(x, y)\to(1,2)}\frac{16x-16-8xy+8y+xy^2-y^2}{12x-12-3xy+3y}= . . . = \frac{2}{3}$

P.K.

vlado_bb

↑ PlusPlusPlus: $\lim_{(x, y)\to(1,2)}\frac{16x-16-8xy+8y+xy^2-y^2}{12x-12-3xy+3y}= \lim_{(x,y) \to (1,2)} \frac{(x-1)(16-8y+y^2)}{(x-1)(12-3y)}= \frac 23$

vanok · 10. 12. 2016 11:51

Poznamka
$\frac{(x-1)(16-8y+y^2)}{(x-1)(12-3y)}=\frac {4-y}3; x\neq 1, y\neq 4$

PlusPlusPlus · 10. 12. 2016 18:48

Děkuji Vám oběma za reakci, jsem potěšen. Přesně tak to bylo konstruované - vytýkání a krácení. Následující příklad již tak triviální není. Chvíli jsem nad jeho konstrukci přemýšlel. Teda alespoň se mě to takto jeví. Pokud Vás příklad zaujme, rád se obohatím o Váš postup řešení příkladu.

$\lim_{(x, y)\to(2,3)} \frac{2x^2y-8xy-3x^2+12x+8y-12}{x^3y-6x^2y+12xy+23x^2-3x^3-56x-8y+44}= . . . = \frac{3}{5}$

Zdravím P.K.

vanok · 10. 12. 2016 19:25

↑ PlusPlusPlus:
Ahoj,
Aj tu mozes zjednodusit tvoj vyraz, $(x-2)^2$ je spolocny faktor.
A tak ako prvu cast cvicenia mozes dat, napr. : Najst a napisat Bezout-ovu relaciu co da do popredia tento najvädci spolocny delitel.

PlusPlusPlus · 10. 12. 2016 21:40

↑ vanok:
Ahoj,

Děkuji za hodnotný příspěvek. Popsal jste to přesně. Příklad navrhuji v rámci cvičení spíš rozšířit o dopočítání exponentu $m$ tak, aby platila rovnice :

$\lim_{(x, y)\to(2,3)} \left[ \frac{2x^2y-8xy-3x^2+12x+8y-12}{x^3y-6x^2y+12xy+23x^2-3x^3-56x-8y+44}+\frac{2}{5} \right]^m= e$ Správný výsledek je: $m=\frac{25}{16y-3xy+9x-48}$

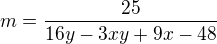
Zdravím P.K.

PlusPlusPlus · 11. 12. 2016 20:24

Dobrý večer,
dnes jsem si našel chviličku a zkonstruoval následující limitu. Návod k řešení: Využijte rozklady 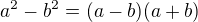$a^2-b^2=(a-b)(a+b)$ a $a^3-b^3=(a-b)(a^2+ab+b^2)$
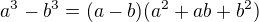
Uvítám, pokud si najdete chviličku k řešení příkladu.

$\lim_{(x, y)\to(2,-1)} \frac{\sqrt{3x^2y-12xy+3x^2-12x+9}-3}{2+\sqrt[3]{2x^2y-8xy+2x^2-8x-8}}= . . . =3$

Zdravím
P.K.

PlusPlusPlus · 12. 12. 2016 17:38

Dobrý večer,

předkládám pro případné zájemce další limitu k řešení...

$\lim_{(x, y)\to(0,1)}\frac{3x^2-(y-1)^2(y-4)^3}{x^2-9(y-1)^2}= . . . = 3$

Zdravím
P.K.

PlusPlusPlus

Dobrý večer,

zkonstruoval jsem následující limitu jedné proměnné se dvěma parametry. Zkusím ještě popřemýšlet o obdobu limity pro dvě proměnné a dva parametry. Uvítám, pokud si najdete čas na řešení a případné uvedení Vašeho postupu výpočtu.

Pro všechna nenulová reálná čísla $p,k\in\mathbb{R}\backslash\{0\}$ platí:

$\lim_{x\to 2} \frac{\sqrt[p]{(3x^2-12x+21)^3}-\sqrt[p]{(2x^2-8x+35)^2}}{\sqrt[k]{4x+8}-\sqrt[k]{(\frac{1}{2}x+3)^2}}= . . . = - \frac{1472}{27} . \frac{k}{p} . \frac{\sqrt[p]{729}}{\sqrt[k]{16}}$

P.K.

PlusPlusPlus

Dobrý večer,

následující limita dvou proměnných je obdobou řešení předcházejícího příkladu s jednou proměnnou. Uvítám, pokud si najdete čas na řešení a případné uvedení Vašeho postupu výpočtu.

Pro všechna nenulová reálná čísla $p,k\in\mathbb{R}\backslash\{0\}$ platí:

$\lim_{(x, y)\to(2,1)} \frac{\sqrt[p]{(x^2y-x^2-4y+8)^3}-\sqrt[p]{(2xy-2x-4y+12)^2}}{\sqrt[k]{9y^2+18xy-18x+72}-\sqrt[k]{(3y+6)^2}}= . . . = \frac{45}{4} . \frac{k}{p} . \frac{\sqrt[p]{64}}{\sqrt[k]{81}}$

P.K.

PlusPlusPlus · 07. 01. 2017 19:17

Dobrý večer,

Zkonstruoval jsem následující limitu s absolutí hodnotou. Pokud se někdo pokusí limitu spočítat, budu velmi potěšen.

$\lim_{x\to3} \frac{|2x^2-12x+18|+|3x-\frac{x^3}{9}-6|}{|\frac{2x-6}{sin(2x-6)}-1|}= . . . = \frac{9}{2}$

P.K.

PlusPlusPlus

Dobrý večer,

Ještě jeden příklad s absolutní hodnotou. Použijte postup bez využití L´H´.

$\lim_{x\to3} \frac{|x^2-x-6|+|x^3-8x^2+19x-12|}{|e^{3x}-e^9|}= . . . = \frac{7}{3e^9}$

P.K.

PlusPlusPlus · 15. 01. 2017 14:27

Zdravím,
když tak přemýšlím o příkladech na limitu funkce jedné proměnné, většinou se najde nějaký způsob k jejímu vyřešení: derivace, Taylor...
Pokusil jsem se zkonstruovat limitu, jejíž řešení tak triviální není. Zde již klasické finty nefungují. Alespoň se mě to takto jeví. Pokusí se následující příklad někdo vyřešit?

$\lim_{x\to2} \left[ e^{x-2}+\frac{sin(x+1)-sin3-(x-2)^2}{x-2}-cos(\frac{x+4}{2})\right]^{\frac{24x}{(cos(3)-12).\left[ ln(2x-1)-ln3+ \frac{4}{3}-\frac{2x}{3}\right] }}= . . . = e^9$

P.K.

Matematické Fórum

#1 11. 11. 2016 22:59

P.K. Limita funkce

#2 11. 11. 2016 23:00

Re: P.K. Limita funkce

#3 12. 11. 2016 12:07 — Editoval PlusPlusPlus (12. 11. 2016 12:08)

Re: P.K. Limita funkce

#4 13. 11. 2016 10:19

Re: P.K. Limita funkce

#5 15. 11. 2016 21:33 — Editoval PlusPlusPlus (17. 11. 2016 22:05)

Re: P.K. Limita funkce

#6 16. 11. 2016 21:59

Re: P.K. Limita funkce

#7 17. 11. 2016 22:01 — Editoval PlusPlusPlus (17. 11. 2016 22:16)

Re: P.K. Limita funkce

#8 22. 11. 2016 17:20 — Editoval PlusPlusPlus (22. 11. 2016 17:23)

Re: P.K. Limita funkce

PlusPlusPlus napsal(a):

#9 06. 12. 2016 18:30

Re: P.K. Limita funkce

#10 09. 12. 2016 16:44

Re: P.K. Limita funkce

#11 09. 12. 2016 17:11 — Editoval vlado_bb (09. 12. 2016 17:11)

Re: P.K. Limita funkce

#12 10. 12. 2016 11:51

Re: P.K. Limita funkce

#13 10. 12. 2016 18:48

Re: P.K. Limita funkce

#14 10. 12. 2016 19:25

Re: P.K. Limita funkce

#15 10. 12. 2016 21:40

Re: P.K. Limita funkce

#16 11. 12. 2016 20:24

Re: P.K. Limita funkce

#17 12. 12. 2016 17:38

Re: P.K. Limita funkce

#18 17. 12. 2016 22:14 — Editoval PlusPlusPlus (18. 12. 2016 21:07)

Re: P.K. Limita funkce

#19 18. 12. 2016 20:53 — Editoval PlusPlusPlus (18. 12. 2016 21:06)

Re: P.K. Limita funkce

#20 07. 01. 2017 19:17

Re: P.K. Limita funkce

#21 07. 01. 2017 21:32 — Editoval PlusPlusPlus (07. 01. 2017 21:45)

Re: P.K. Limita funkce

#22 15. 01. 2017 14:27

Re: P.K. Limita funkce

Zápatí