Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 12. 2016 15:43 — Editoval liamlim (04. 12. 2016 15:57)
Tělesa
Ahoj,
Už nějakou dobu mě zajímají tělesa a došel jsem k něčemu docela zajímavému. Zde píši, abych shrnul své myšlenky a případně byl upozorněn na chybné úvahy.
Nejprve zavedu značení. Nechť  a
a  . Zřejmě platí
. Zřejmě platí  .
.
Zkusme nyní pro obecné  definovat
definovat  . S touto definicí nám kupříkladu vyjde
. S touto definicí nám kupříkladu vyjde  přičemž je splněna důležitá podmínka těles! Totiž distributivita:
přičemž je splněna důležitá podmínka těles! Totiž distributivita: .
.
Nemám dokázáno, že pro  a
a 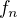 bude platit distributivita, ale velmi v to věřím (pro obecné
bude platit distributivita, ale velmi v to věřím (pro obecné  ). Věřím v to, protože i když definujeme
). Věřím v to, protože i když definujeme  , které nám ukazuje, jak přirozeným způsobem rozšířit definici funkcí i do záporných indexů, distributivitu společně s násobením splňuje.
, které nám ukazuje, jak přirozeným způsobem rozšířit definici funkcí i do záporných indexů, distributivitu společně s násobením splňuje.
Jde vidět, že mnou definované funkce splňují ostatní axiomy těles, které nevyžadují neutrální prvky. Zde mám otázku. Myslíte si, že je možné doplnit neutrální prvky vzhledem ke každé mnou definované operaci? Ideálně tak, aby byly jedinečné?
Totiž takto, platí následující: &
& 
 &
& 
 &
& 
 &
& 
Bohužel nějak hlouběji do struktury funkcí  nevidím. Nemáte někdo lepší vhled? Minimálně pro záporné indexy podle mě budou neutrální prvky nadále existovat. Ale s existencí neutrálních prvků v kladných indexech si nejsem jistý. Díky!
nevidím. Nemáte někdo lepší vhled? Minimálně pro záporné indexy podle mě budou neutrální prvky nadále existovat. Ale s existencí neutrálních prvků v kladných indexech si nejsem jistý. Díky!
edit: oprava indexů
Offline
#2 04. 12. 2016 16:35
Re: Tělesa
Ahoj,
Nemam cas prehlbit tvoje pisanie.
Tu som pisal, zda sa mi o nie com analogickom
http://forum.matweb.cz/viewtopic.php?id=86983
Dobre pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 12. 2016 16:46
Re: Tělesa
↑ vanok:
O tom vláknu vím a četl jsem jej. To co popisuji je, že věřím, že takových dvojic tvořících těleso je nekonečně mnoho a že je mezi nimi nějaký rekurzivní vztah. Jediný problém je v obecném důkazu distributivity a v nalezení neutrálních prvků ke každé takové operaci.
Ten vztah mezi operacemi 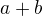 ,
, 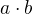 ,
,  , který jsem uváděl, není tak úplně jen od pohledu zřejmý. Je zřejmý až pokud přidáme další operaci
, který jsem uváděl, není tak úplně jen od pohledu zřejmý. Je zřejmý až pokud přidáme další operaci  . Velmi by mě zajímalo, jestli kupříkladu platí nějaká pěkná vlastnost mezi operacemi
. Velmi by mě zajímalo, jestli kupříkladu platí nějaká pěkná vlastnost mezi operacemi  a
a  . To jistě budu zkoušet.
. To jistě budu zkoušet.
Offline
