Matematické Fórum

renzin · 12. 12. 2016 20:38 — Editoval renzin (12. 12. 2016 20:39)

Dobrý den,
mohu se zeptat,jak se nejlépe dobrat postupu,že $\lim_{x\to-\infty }(x+\mathrm{e}^{-x})=\infty$ ?Pořád se pokouším výraz upravovat,ale stale se dostávám k nedefinovaným výrazům.Zdůvodňuji si to tím,že exponenciální funkce roste rychleji než lineární,ale lze to použít jako zdůvodnění?
Děkuji

byk7 · 12. 12. 2016 21:00 — Editoval byk7 (12. 12. 2016 21:08)

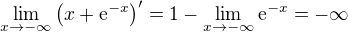Co takto? Pro $x\in(-\infty,0)$ je $$x+\mathrm{e}^{-x}$'=1-\mathrm{e}^{-x}<0$ , tj. funkce je na tomto intervalu klesající (při jízdě zprava doleva jedeme nahoru). Protože $\lim_{x\to-\infty}\left(x+\mathrm{e}^{-x}\)'=1-\lim_{x\to-\infty}\mathrm{e}^{-x}=-\infty$ , je funkce 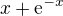$x+\mathrm{e}^{-x}$ shora neohraničená. Odtud a z monotonie už $\lim_{x\to-\infty}x+\mathrm{e}^{-x}=\infty$ .

Otázka je, jestli můžeš použít derivace. :-)

Edit.: Opraveno znaménko.

Blackflower

↑ renzin: Našla som nejakú kalkulačku, čo ukáže aj postup:
link
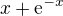Taktiež sa to dá vydedukovať aj z grafu, keď si napríklad vo wolframe nakreslíš funkcie $\mathrm{e}^{-x}$ a $x+\mathrm{e}^{-x}$ na porovnanie, vľavo od osi $y$ vyzerajú veľmi podobne. (Obrázok síce nie je dôkaz, ale môže pomôcť.)
Ja osobne by som asi použila rovnaké zdôvodnenie ako ty.

EDIT: ↑ byk7: ma predbehol, ale nechám to tu.

renzin · 13. 12. 2016 06:28

Oběma Vám moc děkuji. A dá se k výsledku dojít i početně nějakým způsobem?

misaH · 13. 12. 2016 06:55

↑ renzin:

Veď tá kalkulačka (link) od Blackflower ti to ukazuje...

renzin · 13. 12. 2016 07:08

↑ misaH:
To ano, i jsem poděkoval,ale spíše mne zajímá, kdybych například dostal takovýto příklad v nějakém testu a nemohl bych používat kalkulačky či pčítač

Blackflower · 13. 12. 2016 22:32

↑ renzin: Ja osobne by som asi použila argument, ktorý si napísal hneď v úvodnom príspevku. Neviem, či by mi to vyučujúci uznal, je dosť možné, že nie, ale pravdepodobne by mi nenapadol postup, ktorý ponúka kalkulačka.

Pavel · 13. 12. 2016 22:39

↑ renzin:

$\lim_{x\to-\infty }(x+\mathrm{e}^{-x}) =\lim_{x\to+\infty }(-x+\mathrm{e}^x) =\lim_{x\to+\infty }\left[x\cdot\left(-1+\frac{\mathrm{e}^x}{x}\right)\right] =\lim_{x\to+\infty }x\cdot\lim_{x\to+\infty }\left(-1+\frac{\mathrm{e}^x}{x}\right)$

Nyní stačí ukázat, že obě limity vpravo jsou rovny $+\infty$ .

Matematické Fórum

#1 12. 12. 2016 20:38 — Editoval renzin (12. 12. 2016 20:39)

Limita funkce

#2 12. 12. 2016 21:00 — Editoval byk7 (12. 12. 2016 21:08)

Re: Limita funkce

#3 12. 12. 2016 21:06 — Editoval Blackflower (12. 12. 2016 21:06)

Re: Limita funkce

#4 13. 12. 2016 06:28

Re: Limita funkce

#5 13. 12. 2016 06:55

Re: Limita funkce

#6 13. 12. 2016 07:08

Re: Limita funkce

#7 13. 12. 2016 22:32

Re: Limita funkce

#8 13. 12. 2016 22:39

Re: Limita funkce

Zápatí