Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 12. 2016 14:06 — Editoval Welite (07. 12. 2016 14:07)
Výpočet maxima
Zdravím, potřeboval bych vyřešit prakticky uplně identický příklad, jako se řešil zde:
http://forum.matweb.cz/viewtopic.php?id=88298
Nicméně autor zde bohužel nezveřejnil své finální řešení a značení je taky dost zmatené. Vůbec nevím jak z takovou úlohou začít a jak vůbec dopočítat ostatní strany trojúhelníku a zda je vůbec při výpočtu potřebuji. Jediné co chápu je, že musím nějak sestavit funkci pro výpočet maxima ale jak...
Děkuju za každou pomoc.
Offline
#2 11. 12. 2016 22:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet maxima
Zdravím,
v odkazu kolega si způsobil zmatek, že používal stejné označení pro strany v obdélníku a v trojúhelníku (vycházel ze vzorců tak, jak najdeme v tabulkách pro trojúhelník ABC a pro obdélník ABCD). U vás přímo v zadání je na to dokonce pamatováno a trojúhelník ABC, obdélník KLMN. Tedy stačí dobře a přehledně označit. Viz stejná úloha s postupem od kolegy Jj, kolegovi děkuji.
V minulém roce v tomto období jsem posbírala materiály, určitě lze vhodně využit (zejména doporučení o čtení materiálů před vložením dotazu :-)). Děkuji.
Offline
#3 12. 12. 2016 09:18 — Editoval Cheop (12. 12. 2016 13:49)
- Cheop
- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Výpočet maxima
↑ jelena:
Zdravím, pokud něco nepřehlížím, tak maximální obsah obdélníka je 8 cm^2,
ale ten jde vepsat pouze do trojúhelníku pravoúhlého, což je v rozporu se zadáním.
Edit: Tak obdélník s obsahem 8 cm^2 jde umístit do takového trojúhelníku tak, aby vyhovoval zadání (ostroúhlého)
Nikdo není dokonalý
Offline
#5 12. 12. 2016 19:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet maxima
Zdravím,
↑ Cheop: zadání
Do ostroúhlého trojúhelníku ABC, c = 8 cm, vc = 4 cm, vepište obdélník KLMN maximálního obsahu tak, aby úsečka KL byla částí úsečky AB. Určete rozměry takového obdélníku.
skutečně neurčuje jednoznačně trojúhelník ABC (můžeme jen doplnit polohu paty výšky 
, pro kterou bude trojúhelník pravoúhlý s pravým úhlem u vrcholu C). Tedy pokud vyšlo, že maximální obsah je pro stranu obdélníku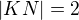 
cm (a obsah je 8 cm^2) - odkaz :-) tak ještě můžeme pokračovat k určení úhlu u vrcholu C (aby trojúhelník byl ostroúhlý). Strana MN je střední příčkou trojúhelníku ABC a tedy by nalezený obdélník šlo vepsat do každého ostroúhlého trojúhelníku s rozměry dle zadání.
Teď otázka, co jsem na oplatku přehlédla já (a proč Tobě vychází pouze jeden ostroúhlý trojúhelník). Kolega Jj také píše, že výsledek nezáleží na umístění bodu C (nezáleží na x-souřadnici, y-souřadnice je dána ).
já jsem před rokem napsal(a):
Jelikož předvánoční čas je náročný na více aktivit, tak už to, prosím, nějak dodělej
:-) tak nějak platí pořád.
Offline
#7 13. 12. 2016 19:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet maxima
↑ Cheop: to je výborné, máme pořádek (naše nejmilejší knihovna to dokonce dala i na letošní PF). Zbývá zjistit, jak je na tom autor tématu - zda lze označit za vyřešené :-) Zdravím.
Offline