Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 12. 2016 18:54
Řešení kombinatorické úlohy
Dobrý večer,
sedím nad jedním příkladem z kombinatoriky a nejsem si jistý správným řešením, ani se mi nikde nepodařilo najít podobný příklad, na kterém bych si své řešení mohl zkontrolovat.
Zadání: Smírčí komise uživatelů operačních systémů pořádá konferenci, na kterou přijelo 6 zástupců MS Windows, 7 Applu a 5 Linuxu. Členy jednotlivých spolků od sebe nebudeme rozlišovat.
b) Kolika způsoby je můžeme rozsadit do sálu, který má 25 (očíslovaných) míst?
c) Každý účastník konference bude mít přednášku. Kolika způsoby můžeme sestavit program přednášek, pokud chceme, aby hned za sebou nebyly dvě přednášky zastánců Applu?
U b) si myslím, že by to mohla být kombinace bez opakování, tedy (25 nad 18). Velmi pravděpodobně je to ale špatně :) No a u c) nemám ani moc žádný tip...
Budu rád za každou radu, díky!
Offline
#3 15. 12. 2016 19:31
Re: Řešení kombinatorické úlohy
b) je rozsirenie kombinacnych cisel: http://mathworld.wolfram.com/Multinomia … cient.html s tym ze pridas 7 prazdnych miest
c) skladas 2 veci: rozdelenie 11 neapplovych prednasok do 8 blokov tak ze 6 blokov je neprazdnych a 2 mozu byt prazdne (zaciatocny a koncovy), a rozdelenie 5 prednasok medzi tych 11 hocijako
Offline
#4 23. 07. 2017 01:42
- check_drummer
- Příspěvky: 4901
- Reputace: 105
Re: Řešení kombinatorické úlohy
↑ Xellos:
Ahoj, k c: Tak, jak to píšeš, tak není zřejmé, jak těch 8 bloků sestrojit. spíš by stačilo nejprve rozvrhnout 6+5 neapplových přednášek a následně do mezer mezi něktreými z nich (resp. na začátek nebo na konec) umístit applové - a to lze provést celkem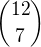 
způsoby, jak ty applové do mezer umístit, protože mezer je 12 (resp. 10 +2 na okraji).
"Máte úhel beta." "No to nemám."
Offline
#5 02. 08. 2017 13:19
Re: Řešení kombinatorické úlohy
b)
5 + 6 + 7 = 18
mist 25
25 - 18 = 7
1 | 1 | 1 | 7 - jakoze mas 10 lidi na 10 zidli
Za predpokladu
- chces, aby byli u sebe
- je fuk, jestli je mezi nimi volne misto
- je fuk, jestli se na zidlich nejak promichaji., jen jim chces rezervovat prislusny pocet zidli
c)
To musim promyslet. To muze vypadat takto, ale i takto
123123
121212
Offline