Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hodnost, jádro a defekt lineárního funkcionálu
#1 17. 12. 2016 18:02 — Editoval dominiksep (17. 12. 2016 18:03)
- dominiksep
- Příspěvky: 54
- Reputace: 0
Hodnost, jádro a defekt lineárního funkcionálu
Ahoj,
potřebuji pomoct s následujícím příkladem.
Nechť 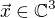 ,
,  , přičemž
, přičemž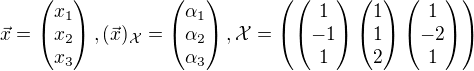
Zatím jsem vypočítal hodnost (1, protože zobrazení není nulové) a defekt (z 2. věty o dimenzi 2). Nevím ale, jak určit bázi jádra.
Vadí mi, že se tam míchají souřadnice ze standardní a x-ové báze.
Děkuji
Offline
#2 17. 12. 2016 18:50
Re: Hodnost, jádro a defekt lineárního funkcionálu
↑ dominiksep:,
Ahoj, skontroluj text cvicenia. Nie je to jasne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 18. 12. 2016 13:37
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Hodnost, jádro a defekt lineárního funkcionálu
Nechť 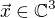 (vektorový prostor nad tělesem komplexních čísel),
(vektorový prostor nad tělesem komplexních čísel), je lineární funkcionál,
je lineární funkcionál,  a
a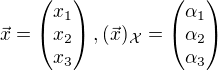 , kde
, kde 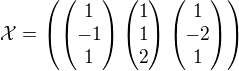 je báze vektorového prostoru
je báze vektorového prostoru 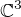 a
a 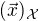 souřadnice vektoru v této bázi.
souřadnice vektoru v této bázi.
Zatím jsem vypočítal hodnost (1, protože zobrazení není nulové) a defekt (z 2. věty o dimenzi 2). Nevím ale, jak určit bázi jádra.
Vadí mi, že se tam míchají souřadnice ze standardní a x-ové báze.
Děkuji
Offline
#4 18. 12. 2016 14:01
Re: Hodnost, jádro a defekt lineárního funkcionálu
↑ dominiksep:,
Cize si popisal hlavny problem.
Vsak aj to  nie je dobre definovane.
nie je dobre definovane.
Ako je to polozene, neviem s tym nic robit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hodnost, jádro a defekt lineárního funkcionálu
