Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 25. 12. 2016 20:07
#5 26. 12. 2016 01:06
Re: Zobrazení matice v bázi
↑ vytautas:
Ten druhý obrázek, co jsem poslal je celé zadání.
Přidávám ještě celý postup výpočtu:
Potřebuji vědět, jak se dopracovalo k té červeně podtržené matici (ϕ)α,α. Zbytek dopočítat umím
Offline
#6 26. 12. 2016 02:39
Re: Zobrazení matice v bázi
Ahoj ↑ orisk:,
Riesenie je okamzite, od okamihu, ked si napisal text cvicenia.
Mas dani v texte popis tvojeho zobrazenia. ↑ orisk:
Ide o osovu symetriu priamky p.
Text cvicenia ti da prvy vektor bazy v1, pouzit en v rieseni
Vyber dvoch ostatnych vektorov v2,v3 je tu vybrany vdaka definicii osovej sumernosti. (Ich obrazy su....)
V tejto bazy mas okamzite tvoju hladanu maticu ( pociarchnutu cervenov)
Zvysok je klasicke pouzitie zmeny baz....
Pochopitelne kazdy iny mozny vyber v1,v2,v3. by ti dal iny, ale analogicky postup co by ta doviedol k tomu istemu konecnemu vysledku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 26. 12. 2016 12:22
Re: Zobrazení matice v bázi
↑ orisk:
je mi jasné, čo potrebuješ vedieť. Otázka smerovala na teba. Ako je teda definovaná matica  ?(čakám tvoju odpoveď, nie obrázok s riešením) potom môžme pokračovať s riešením.
?(čakám tvoju odpoveď, nie obrázok s riešením) potom môžme pokračovať s riešením.
Per aspera ad astra
Offline
#8 26. 12. 2016 15:14
Re: Zobrazení matice v bázi
↑ vanok:
Mám směrový vektor v1 a na něj kolmé vektor v2,v3. Nevím, jak pomocí těch vektorů provést osovou symetrii.
↑ vytautas:
Matice  je definovaná v zadání jako symterie podle přímky p.
je definovaná v zadání jako symterie podle přímky p.
Offline
#9 26. 12. 2016 23:56
Re: Zobrazení matice v bázi
↑ orisk:
ok, teda, treba si asi ujasniť pojmy
zobrazenie  je zrkadlenie podľa priamky
je zrkadlenie podľa priamky  . Matica
. Matica  je matica prechodu zobazenia od báze
je matica prechodu zobazenia od báze  k báze
k báze  a je definovaná ako
a je definovaná ako ![kopírovat do textarea $\varphi_{\alpha,\alpha}=([\varphi(v_1)]_\alpha|[\varphi(v_2)]_\alpha|[\varphi(v_3)]_\alpha)$](/mathtex/47/475f5dcad70ed6e9881b92e82edb2651.gif) , kde
, kde ![kopírovat do textarea $[v]_\alpha$](/mathtex/f6/f672045911ebb3cfe3dcf4c4c920167a.gif) sú súradnice vektora v báze
sú súradnice vektora v báze  .
.
A teraz si už len stačí nakresliť situáciu, uvedomiť si, čo robí  s vektorom
s vektorom 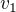 a s vektormi
a s vektormi 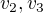 (teda ako vyzerá
(teda ako vyzerá 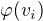 pre
pre  ).
).
z toho ti už vyplynie prečo vyzerá matica  tak, ako vyzerá.
tak, ako vyzerá.
Per aspera ad astra
Offline
#10 27. 12. 2016 00:07
Re: Zobrazení matice v bázi
↑ vytautas: ,↑ orisk:
Ano, tu ak mas sponmienky z geometrie smerovy vektor v1 sa tvojou symetriou nemeni.
A kolme vektory v2,v3 na v1, sa danou symetriou transformuju na -v2,-v3.
Zvysok je ozaj hracka.... skutocne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 27. 12. 2016 00:13
Re: Zobrazení matice v bázi
↑ vytautas:
Moc děkuju za snahu, ale příliš tomu, co tu popisuješ nerozumím. Potřeboval bych to vysvětlit polopaticky, jinak na to asi nikdy nepřijdu.
Offline
#12 27. 12. 2016 00:26
Re: Zobrazení matice v bázi
↑ orisk:
musíš mať nejaké základy lineárnej algebry, bez toho to nejde. Ak ti nie sú jasné pojmy, preštuduj si skriptá. Ak ti nie je jasný niektorý krok, tak sa pýtaj konkrétne na krok.
Per aspera ad astra
Offline
#13 27. 12. 2016 16:19
Re: Zobrazení matice v bázi
↑ vanok:
Jestli to dobře chápu, tak vektor v1 zůstává tedy stejný (přímka p), tzn(3,0,-1) a vektory v2 a v3 se symetricky otočí, takže budou mít hodnotu v2=(-1,0,-3) a v3=(0,-1,-1).
Ale pořád nechápu, jak z toho dostanu tu diagonální matici:
1 0 0
0 -1 0
0 0 -1
Žádnou operací s maticemi se mi to nepodařilo.
Offline
#14 27. 12. 2016 16:48
Re: Zobrazení matice v bázi
↑ orisk:,
V bazi (v1,v2,v3)
Vector v1=1v1+0v2+0v3 ma suradnice (1,0,0)
Vektor v2= 0v1+1v2+0v3 ....
Staci?
Kontrola.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 27. 12. 2016 21:03
Re: Zobrazení matice v bázi
No oznacenie nie je dokonale.
V bazy 
 atd.
atd.
No ked je jasne o aku bazu ide piseme jednoducho...=(1,0,0). Co tu bolo jasne povedane ....ale pre opatrnych a vahajucych ludi je to opatrnejsie pisat z tym indexom. ( hovori sa o " abus de language"... a je uzitocne porozmyslat, aj preco taketo nepresnosti mozu byt uzitocne aj na pokrok vedy.... )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 28. 12. 2016 00:21
Re: Zobrazení matice v bázi
↑ orisk:
ako som písal vyššie, definícia je takáto![kopírovat do textarea $\varphi_{\alpha,\alpha}=([\varphi(v_1)]_\alpha|[\varphi(v_2)]_\alpha|[\varphi(v_3)]_\alpha)$](/mathtex/47/475f5dcad70ed6e9881b92e82edb2651.gif)
Máš zrkadlenie podľa priamky  , ktorá má smerový vektor
, ktorá má smerový vektor 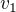 . A čo robí zrkadlenie podľa priamky s bodmi na priamke ? No, nerobí s nimi nič, ostávajú tam kde sú. Teda
. A čo robí zrkadlenie podľa priamky s bodmi na priamke ? No, nerobí s nimi nič, ostávajú tam kde sú. Teda 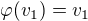 , čo sa ale rovná
, čo sa ale rovná  . Teda
. Teda ![kopírovat do textarea $[\varphi(v_1)]_\alpha=[v_1]_\alpha= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$](/mathtex/d4/d4c2535bc23800eb8573900d36c3817d.gif)
preto je prvý stĺpec taký, aký je.
ďalej keď vieš, že 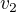 je kolmý na priamku
je kolmý na priamku  , tak ako vyzerá obraz
, tak ako vyzerá obraz 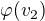 .Je to zrkadlenie, teda ho prevedie na
.Je to zrkadlenie, teda ho prevedie na  násobok, teda
násobok, teda 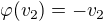 . Teda vyjadrená v báze
. Teda vyjadrená v báze  je to
je to 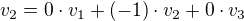 a tak súradnice vzhľadom k
a tak súradnice vzhľadom k  sú
sú ![kopírovat do textarea $[\varphi(v_2)]_\alpha=[-v_2]_\alpha=\begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix}$](/mathtex/e8/e811b92496f339504a3b8e0f6b32a101.gif)
rovnako pre 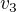 , až na to, že
, až na to, že 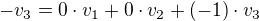 a tak súradnice vzhľadom k
a tak súradnice vzhľadom k  sú
sú ![kopírovat do textarea $[-v_3]_\alpha = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} $](/mathtex/28/28f68a45f97b1810a9902a6c116edb33.gif)
Dôkladne ti doporučujem prejsť si základy lingebry, toto je len prepis definícii, bez tohto sa nepohneš ďalej.
Per aspera ad astra
Offline



![kopírovat do textarea $ \varphi_{\alpha,\alpha}=\[\varphi\]_\alpha^\alpha$](/mathtex/e1/e17f26707ca6ec043036fdf3f4d6c7ce.gif) ?
?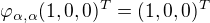 ...atd
...atd