Matematické Fórum

holyduke · 31. 12. 2016 09:48

Ahoj,

Jak se prosim určí obor konvergence této řady?

$\sum_{k=1}^{\infty }\frac{x^{k}}{1+x^{2k}}$

Eratosthenes · 31. 12. 2016 13:19

ahoj ↑ holyduke:

vzpomeň si na vzoreček pro součet geometrické řady a podmínky, za kterých geometrická řada konverguje.

holyduke

↑ Eratosthenes:
Asi jsem mimo, moc nevím, kam tím míříš. Ten výraz je sice trochu podobný součtu NGŘ, ale byl by tam kvocient $-x^{2k}$ . Což je asi blbost.

Zkoušel jsem podílové kritérium, ale to mi vyšlo 1 pro všechna x, takže nic moc

Eratosthenes · 01. 01. 2017 12:50

↑ holyduke:

Proč si myslíš, kvocient $-x^{2k}$ je blbost?

holyduke · 01. 01. 2017 13:00

↑ Eratosthenes:
Protože kvocient nemůže obsahovat "proměnnou" $k$ .

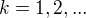$|-x^{2k}|<1$ , kde $k=1,2,...$ řešit neumím

Pritt · 01. 01. 2017 13:44

↑ holyduke:

Ahoj, mělo by to jít i přes Raabeovo kritérium, respektive zobecněné Raabeovo kritérium.

Eratosthenes · 01. 01. 2017 13:48

↑ holyduke:

tak to já sice umím -

$|-x^{2k}|<1 \Rightarrow |-x|^{2k}<1 \Rightarrow |-x|<1 \Rightarrow |x|<1$

ale to není úplně ono. Ten vzoreček totiž není

$s=\sum \frac {a_0} {1 - q}$

ale

$s=\frac {a_0} {1 - q}$

Takže bych spíš přemýšlel nad

$s=a_0\sum q^k$

Xellos · 01. 01. 2017 14:20

Rozober osobitne pripady $|q|<1,=1,>1$ . Vyuzi ze $\frac{q^k}{1+q^{2k}} < \mathrm{min}\left(\frac{q^k}{1},\frac{q^k}{q^{2k}}\right)$ .

holyduke · 01. 01. 2017 14:53

↑ Xellos:
Díky, ted už se mi to podařilo dokončit. Zajímalo by mě, jak bys dál pokračoval ↑ Eratosthenes:? Nic kloudného mě nenapadlo.

Eratosthenes

↑ holyduke:
$\sum_{k=1}^{\infty }\frac{x^{k}}{1+x^{2k}}=$

$\sum_{k=1}^{\infty }[ {\frac x {\sqrt[k]{1+x^{2k}}} ] ^k}$

$a_0=1; q=\frac x {\sqrt[k]{1+x^{2k}}}$

$|x|\le 1\Rightarrow |q|=\frac {|a|} b ; |a|\le 1; b>1 \Rightarrow |q|<1$

$|x|>1\Rightarrow |q|=\frac {|x|} {\sqrt[k]{1+x^{2k}}}<\frac {|x|} {x^2}=\frac 1 {|x|} <1$

tj. konverguje pro každé x :-)