Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 01. 2017 08:06 — Editoval vanok (02. 01. 2017 10:02)
Re: Matice zobrazení
Anoj ↑ Exille:,
Tvoja matica v tvojom texte je matica tvojej projekcie ak baza  je vybrana napr. tak, ze je je vytvorena normalnym unitarnym vektorom
je vybrana napr. tak, ze je je vytvorena normalnym unitarnym vektorom  na danu rovinu a dvomi ortonornalnymi vektormy v danej rovine .
na danu rovinu a dvomi ortonornalnymi vektormy v danej rovine .
( co je inspirovane definiciou danej projekcie)
No vsak najrychlejsie ( zda sa mi) je postupovat napriklad takto.
Sme v  , a oznacme danu rovinu
, a oznacme danu rovinu 
Ortogonal roviny  je priamka
je priamka , ktorej ortonormalna baza je
, ktorej ortonormalna baza je  , kde
, kde 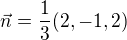 .
.
Preto 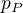 ortogonalna projekcia na priamku
ortogonalna projekcia na priamku  je taka, ze pre kazdy vektor
je taka, ze pre kazdy vektor 
( pochopitelne, znacim ako je zvykom, takto  scalarny sucin)
scalarny sucin)
Akoze, 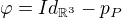
Tak teraz ti necham radost ukoncit dane cvicenie.(3 riadky stacia!)
( pripominam, ze na konci 60 tich rokov minuleho storocia, = doba tzv. "Modernej matematiky", sa taketo cvicenia robili v skoro celej Europe na konci strednej skoly ... no teraz iste az v prvom rocniku VS)
Pochopitelne, je mozne riesit cvicenie aj inac, ako napr vdaka pociatocnej poznamke.
A aby som nezabudol, vsetko najlepsie do noveho roku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 02. 01. 2017 12:58
Re: Matice zobrazení
Pre tych co to zaujima, pridam postup aj na tu druhu metodu o ktorej som vyssie pisal.
Preto najdeme jednu orthogonalnu bazu priestoru 
Na to veznime najprv jednu jeho lubovolnu bazu lubovolnu , napr. 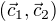 , kde
, kde  a orthogonalizujme ju na
a orthogonalizujme ju na 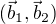 , kde
, kde 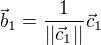 a
a 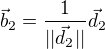 kde
kde  .
.
Potom pre kazdy vector 
Necham vas urobit vypocty, a overit, ze vam to da pochopitelne ten isty vysledok predosla metoda.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 02. 01. 2017 19:14 — Editoval Eratosthenes (02. 01. 2017 19:15)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Matice zobrazení
Ahoj ↑ Exille:,
já přidám ještě třetí možnost:
Hledanou matici označme M. Kolmá projekce do roviny je projekce ve směru jejího normálového vektoru, v našem případě ve směru n = (2;-1;2). Tento vektor se promítne na vektor nulový, tj. platí
o = M.n (1)
Dále najdeme dva libovolné lineárně nezávislé směrové vektory r, s dané roviny - ty jsou kolmé na n, takže je najdeme z podmínek <r;n>=<s;n>=0. Tyto vektory se zobrazí samy na sebe, tj.
r = M.r (2)
s = M.s (3)
Z rovnic (1) (2) (3) obdržíme maticovou rovnici
(o r s) = M . (n r s)
a hledaná matice je M =(o r s).(n r s)^(-1)
PS: Pro přehlednost jsem vynechal značky transpozic - o, r, s, n jsou tedy sloupce a (o r s), (n r s) čtvercové matice sestavené z těchto sloupců.
Budoucnost patří aluminiu.
Online
#5 02. 01. 2017 21:46
Re: Matice zobrazení
Pozdravujem ↑ Eratosthenes:,
Ano dal si nam tu peknu intuitivnu metodu.
Mozes upresnit matice prechodu do stardantnej baze?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


