Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 01. 2008 16:00
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Limita
vynásobit a vydělit výrazem (a^2+ab+b^2), kde a a b jsou první a druhý člen v té limitě. Potom použít vzorec (a^3-b^3)=(a-b)(a^2+ab+b^2), něco se odečte a bude to v pohodě.
Offline
#7 07. 01. 2008 22:43 — Editoval jelena (07. 01. 2008 22:43)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
Ani trochu neotravujes, ale driv jsem nemela cas (snad ta pisemka nebo co nebylo dnes :-(
nejdriv vytknu x^3 v zavorkach pod mocninami![kopírovat do textarea $\frac{5x^2}{4x^2 + 2x\sqrt[3]{x^3(8 - \frac{5}{x})}+ \sqrt[3]{(x^3(8 - \frac{5}{x}))^2}}$](/mathtex/8e/8e9bc2d519856c7056f4b9be9a5e7257.gif)
ted vytahnu x z mocnin![kopírovat do textarea $\frac{5x^2}{4x^2 + 2x^2\sqrt[3]{8 - \frac{5}{x}}+ x^2\sqrt[3]{(8 - \frac{5}{x})^2}}$](/mathtex/78/7842d78220c871e9e1fbe99b1ce2e0e3.gif)
a ted podelim kazdy clen x^2 - cimz dostanu ten vysledek, co mam uvedeny.
Abych rekla pravdu, tak ja delim rovnou, aniz bych to tak rozepisovala, ale za tim je urcity cvik, ze zacatku to asi budes muset trochu rozepisovat, v cem preji hodne zdaru :-)
Offline
#8 08. 01. 2008 16:21 — Editoval Okaz (08. 01. 2008 16:23)
Re: Limita
Ne v pohode, zkouska az pristi pondeli, ale mezitim dalsi 2, takze se musim ucit na vsechno, ted sem to sice pochopil, ale vypocitat podobnej priklad jak to tak vypada je stejne nad moje sily, takze musim doufam ze zrovna tohle nevyfasuju. Ale aspon vim princip jak na to
Jinak diky moc
Offline
![kopírovat do textarea $\lim_{x\rightarrow \infty} (2x - \sqrt[3]{8x^3 - 5x^2})$](/mathtex/5f/5fb2397f2d205ba35f722c63581665c4.gif)
![kopírovat do textarea $\frac{(2x - \sqrt[3]{8x^3 - 5x^2})(4x^2 + 2x\sqrt[3]{8x^3 - 5x^2}+ \sqrt[3]{(8x^3 - 5x^2)^2}}{4x^2 + 2x\sqrt[3]{8x^3 - 5x^2}+ \sqrt[3]{(8x^3 - 5x^2)^2}}$](/mathtex/f5/f51f53a5283f2b5afc31f8b3cf37e7ac.gif)
![kopírovat do textarea $\frac{(8x^3 - (8x^3 - 5x^2)}{4x^2 + 2x\sqrt[3]{8x^3 - 5x^2}+ \sqrt[3]{(8x^3 - 5x^2)^2}}$](/mathtex/51/51feccb0adec9346a43cebd90ecd03b3.gif)
![kopírovat do textarea $\frac{5x^2}{4x^2 + 2x\sqrt[3]{8x^3 - 5x^2}+ \sqrt[3]{(8x^3 - 5x^2)^2}}$](/mathtex/d9/d950421954dbc30d3a84fc045f029b63.gif)
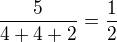 ale tento konec bych radej prekontrolovala
ale tento konec bych radej prekontrolovala