Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » důkaz teorie čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 01. 2017 11:36 — Editoval liamlim (06. 01. 2017 22:50)
důkaz teorie čísel
Zdravím!
Prosím o nápad, jak by se dokázalo tvrzení, které podle všeho platí pro obecné  , já mám ale pouze náznak důkazu pro prvočíselná a nejsem ani schopen zobecnit jej na přirozená čísla.
, já mám ale pouze náznak důkazu pro prvočíselná a nejsem ani schopen zobecnit jej na přirozená čísla.
Dokažte pro libovolné přirozené  , že
, že 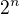 dělí
dělí 
Offline
- (téma jako vyřešené označil(a) liamlim)
#2 06. 01. 2017 13:25
#3 06. 01. 2017 21:56 — Editoval Brano (06. 01. 2017 21:57) Příspěvek uživatele Brano byl skryt uživatelem Brano. Důvod: chybny navod, ktory sa neda nejak jednoducho opravit.
#4 06. 01. 2017 22:24 — Editoval liamlim (06. 01. 2017 22:31)
Re: důkaz teorie čísel
↑ Rumburak:
Mně se to toho roznásobení právě původně vůbec nechtělo, protože jsem si nemyslel, že by k něčemu vedlo. Teď to zkouším a dostal jsem se k něčemu jako: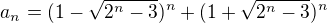


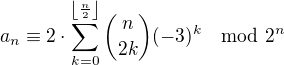
Teď ale úplně dobře nevidím, jak mi toto pomůže.
edit: ale aspoň vidím, že by šlo nejspíše "zhezčit" zadání. Nejspíše by fungovalo, kdybych  v zadání nahradil
v zadání nahradil 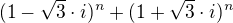 , což skutečně vypadá hezčeji.
, což skutečně vypadá hezčeji.
Offline
#6 07. 01. 2017 00:14
Re: důkaz teorie čísel
No. Vidim ze vyriesene ale aj tak napisem svoje riesenie.
Pouzime rekurzivny vzorec na binomicke koeficienty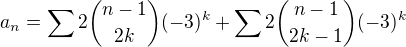
kde  ide cez vsetky cele cisla. Prva suma je
ide cez vsetky cele cisla. Prva suma je  . Druha suma sa da prepisat opat ako
. Druha suma sa da prepisat opat ako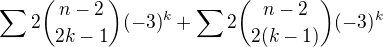
kde druhy clen je  . Prvu sumu zasa rozpiseme podobne a dostaneme
. Prvu sumu zasa rozpiseme podobne a dostaneme 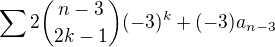 , atd.
, atd.
Eventualne dostaneme rekurentny vzorec 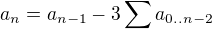 , resp.
, resp. 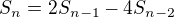 kde
kde 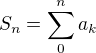 . Tu uz explicitne riesenie vieme, ale ani nam ho netreba - vidno ze
. Tu uz explicitne riesenie vieme, ale ani nam ho netreba - vidno ze 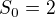 a
a  je nasobok
je nasobok  , preto
, preto 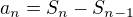 je delitelne
je delitelne 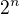 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » důkaz teorie čísel (TOTO TÉMA JE VYŘEŠENÉ)
