Matematické Fórum

vytautas · 21. 01. 2017 21:18

Zdravim

chcel by som sa spytat, ako by sa dokazalo tvrdenie:

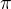Nech $\mathcal{F}$ je system mnozin uzavrety na prieniky ( $\pi$ -system)

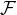potom $\delta(\mathcal{F}) = \sigma(\mathcal{F})$ , kde $\delta()$ je najmensi Dynkinov system obsahujuci $\mathcal{F}$ a podobne $\sigma()$ je najmensia 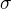$\sigma$ -algebra obsahujuca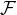 $\mathcal{F}$

Dakujem

Bati · 21. 01. 2017 23:22

Ahoj ↑ vytautas:,
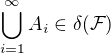pí-systém je uzavřený jen na konečné průniky. Pokud něco nepřehlížím, stačí ti dokázat, že $\delta(\mathcal{F})$ je sigma-algebra, tj., že $\bigcup_{i=1}^{\infty}A_i\in\delta(\mathcal{F})$ . No, ale co si to sjednocení napsat takhle: $\bigcup_{i=1}^{\infty}A_i=\bigcup_{i=1}^{\infty}(A_i\cap\bigcap_{j=1}^{i-1}A_j^c)$ ?
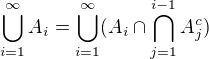Průniky patří do systému, zdají se mi disjunktní, takže výsledek taky padne do stejného systému.

vytautas · 22. 01. 2017 00:43

↑ Bati:

toto som nasiel aj na https://proofwiki.org/wiki/Dynkin_System_Closed_under_Intersections_is_Sigma-Algebra

lenze, my mame definovany Dynkinov system ako $D \subset 2^X$ taku, ze splnuje

$\emptyset,X \in D$

$A,B \in D, B \subset A \Rightarrow A-B \in D$

$A_j \in D$ po dvoch disjunktne, tak $\bigcup^{\infty}_{j=1} A_j \in D$

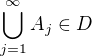
preslo by to aj pri tejto definicii ? nevidim to v tom uplne

dakujem

Bati · 22. 01. 2017 09:47

↑ vytautas:
Ty definice jsou přece ekvivalentní. Pokud chceš vyloženě použít tu vaší, tak místo toho co jsem napsal vezmi
$\bigcup_{i=1}^{\infty}(A_i\cap\bigcap_{j=1}^{i-1}(X\setminus A_j))$

vytautas · 22. 01. 2017 10:07

↑ Bati:

Ok dakujem, to je to, co som potreboval

vytautas · 22. 01. 2017 12:33

↑ Bati:

Este som nasiel jeden zadrhel. Mam $\mathcal{F}$ uzavrety system na prieniky. Ako z toho dostat, ze aj $\delta(\mathcal{F})$ je uzavrety na prieniky ?

Matematické Fórum

#1 21. 01. 2017 21:18

Dynkinov systém

#2 21. 01. 2017 23:22

Re: Dynkinov systém

#3 22. 01. 2017 00:43

Re: Dynkinov systém

#4 22. 01. 2017 09:47

Re: Dynkinov systém

#5 22. 01. 2017 10:07

Re: Dynkinov systém

#6 22. 01. 2017 12:33

Re: Dynkinov systém

Zápatí