Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 01. 2017 23:58
- Dada-ZOO

- Zelenáč
- Příspěvky: 21
- Škola: Česká zemědělská univerzita v Praze
- Pozice: student
- Reputace: 0
definičný obor
Zdravím, chcela by som sa spytat pre objasnenie na pár vecí. Týka sa to definičného oboru. Narazila som na príklad so zlomkom, kde v menovateli bola odmocnina.
Vieme, že pri definičnom obore platia podmienky ze menovatel sa nesmie rovnat 0 a parne odmocniny su vacsie alebo rovne 0.
Ja som to riesila metodou nulovych bodov a vysiel mi vysledok toho menovatela 1 a 3. Vysledok je teda sam o sebe D(f) = (1,3). Ja som to dobre vypocitala a chcem sa spytat, kedze teoreticky ten menovatel ma akoby dve podmienky v jednom ak chápete. Tak sa chcem spytat, preco ten vysledok vysiel tak a nie ze dam D(f)= <1,3>? Teda vysledok kedy tie cisla nerovnicu splnaju?
Snad mi rozumiete, proste preco maju byt tie klasicke zatvorky tam....Alebo mali oni zly vysledok?
Nejake moje selske vysvetlenie ma napada,ale radsej by som to odborne vedela ;)
Dakujem pekne...:)
Offline
#2 22. 01. 2017 08:23
Re: definičný obor
↑ Dada-ZOO:
Nejlepší asi bude názorný příklad.
Mějme funkci 
Pro určení Df máš dvě podmínky (první pro sudou odmocninu, druhou pro jmenovatele)
Obě podmínky musí platit současně
Z první máš ![kopírovat do textarea $x\in[1;3]$](/mathtex/8c/8c643086cc8a42bb21176b489554e53f.gif) , z druhé
, z druhé  ,
, 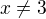
A to jednoduše znamená, že z toho intervalu musíš krajní body vyloučit.
Takže 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 22. 01. 2017 09:22 — Editoval misaH (22. 01. 2017 09:23)
- misaH
- Příspěvky: 13467
Re: definičný obor
↑ Dada-ZOO:
Veď ten definičný obor má nejakú definíciu, podľa niečoho ho hľadáš.
Sú to všetky tie hodnoty nezávisle premennej (obvykle x), pre ktoré sa (podľa daného predpisu) dajú vypočítať hodnoty závisle premennej (obvykle y).
V menovateli nesmie byť 0 nie preto, lebo to tak nariadil niekto zo svojvôle, ale preto, že v prípade 0 v menovateli by si vlastne mala deliť nulou no a taká úloha nemá riešenie, hodnota výrazu s 0 v menovateli sa nedá vypočítať. Preto tie hodnoty x, ktoré z menovateľa urobia 0 nemôžu byť podľa definície D(f) v definičnom obore.
Nestaraj sa o smiešne formality alebo čo. Ak sa pre nejaké x nedá vypočítať y, tak to x nepatrí do D(f). Hotovo.
Offline

 má byt výsledok: D(f)=(-3,
má byt výsledok: D(f)=(-3, )
)  (4, ∞).
(4, ∞).