Matematické Fórum

kompas · 29. 01. 2017 15:17

Ahoj :)

Měl bych tu dotaz na zadání: Najděte bázi vektorového prostoru V=(u1,u2,u3), která obsahuje vektor v.
u1=(1,3,5)
u2=(3,9,15)
u3=(1,0,2)
v=(8,25,40)

dosadím si do matice
(8 25 40)
(1 3 5)
(1 0 2)
(3 9 15)

poslední řádek škrtnu a dále udělám GEM a vznikne mi matice
(8 25 40)
(0 1 0)
(0 0 -3)

Tudíž vím, že vektory: u1,u2, v jsou LN, ale nevím jak bych měl postupovat dál....Vím jen, že by úloha neměla mít řešení, ale nevím z jakého důvodu.....Prosil bych o zdůvodnění pokud by se někdo našel, tak ochotný :)

vytautas · 29. 01. 2017 16:13

↑ kompas:

Ahoj

podla def. maticoveho nasobenia je uloha ekvivalentna s hladanim riesenia sustavy rovnic, kde stlpce matice sustavy su vektory 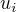$u_i$ a prava strana je $v$ , najprv predsa musime vediet, ci vobec nas vektor $v$ patri do toho vektoroveho priestoru, inak nie je sanca najst bazu,ktora ho obsahuje. uz po prvom kroku GEM je vidiet, ze uloha nema riesenie, teda $v \not \in V$ , teda taka baza neexistuje.

vanok · 29. 01. 2017 19:09

Ahoj ↑ kompas:,
Tvoja metoda hladana bazy je jedna mozne cesta.
Ale co chyba, je vysvetlenie postupu ... ako aj tvojho textu.
Ako si prisiel na to, ze cvicenie, nema riesenie?

Podla textu mas nast jednu bazu priestoru V, ktore jeden prvok je v.
I ked mas prvky riesenia, tak to treba skutocne zvovodnit.

Tu mas jeden mozny postup.
1) ukaz, ze V ma dim 2.
2) najdi jednu jeho bazu
3) ukaz, ze v je vo V
4) podla teoremy konstrukcie baz vytvor novu bazu priestoru V,kde je v jeden clen a vyuzi 2)
5) skuska povinna

Matematické Fórum

#1 29. 01. 2017 15:17

báze vektorového prostoru, která obsahuje vektor v

#2 29. 01. 2017 16:13

Re: báze vektorového prostoru, která obsahuje vektor v

#3 29. 01. 2017 19:09

Re: báze vektorového prostoru, která obsahuje vektor v

Zápatí