Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 25. 01. 2017 20:30 — Editoval vanok (25. 01. 2017 20:43)
Re: Wronskian
Ahoj
Integral e^{2x}dx=?
C2, tvoj vypocet je chybny uz od determinantu
Ale pozor tu v part. rieseni e^{-x} nie je cast riesenia (je v hom. rieseni, ) cize....c
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 27. 01. 2017 20:08 — Editoval vanok (28. 01. 2017 02:52)
Re: Wronskian
↑ Elisa:,
Tak podla najdenych vysledkov partiikuliarne riesenie je 
A vseovecne riesenie to dopln sama.
Poznamka, v partikularnom rieseni mas clen z  to vobec nevadi, lebo ten mozes aj kludne vynechat, lebo
to vobec nevadi, lebo ten mozes aj kludne vynechat, lebo  je koren charakteristickej rovnice.
je koren charakteristickej rovnice.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 28. 01. 2017 02:50
Re: Wronskian
Poznamka, metoda pouzita v cviceni sa vola variacia konstant ( alebo parametrov).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 30. 01. 2017 22:11
Re: Wronskian
Videli ste aj ine metody?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 01. 02. 2017 12:32
Re: Wronskian
Poznamka,
Skuska ta presveci o spravosti vypoctu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



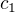 je zle
je zle 
 teda aj nasledujuci integral bude iny
teda aj nasledujuci integral bude iny a potom
a potom