Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 05. 2009 12:07 — Editoval PitBull~--! (08. 05. 2009 12:07)
- PitBull~--!
- Příspěvky: 208
- Reputace: 0
injukce
jak dokazu aby pro kazde 
: .png)
delitelny 5ti ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#2 08. 05. 2009 12:17 — Editoval Marian (08. 05. 2009 12:21)
Re: injukce
↑ PitBull~--!:
Ono to nebude injukce, ale indukce. Otestuješ, zda-li je tvé tvrzení správné pro n=1 (tzv. základ indukce). Pokud ano (to je tvůj případ), potom se předpokládá (tzv. indukční předpoklad), že tvé tvrzení platí pro nějaké fixní číslo n. Zkoumá se, zda-li z tohoto předpokladu nelze rozšířit platnost tvrzení i na hodnotu n+1 (tzv. indukční krok).
Bude
Ale první sčítanec je podle předpokladu dělitelný pěti a druhý (ten dlouhý) se dá po rozepsání binomických koeficientů napsat ve tvaru 5*K, kde K bude nějaké přirozené číslo. Jinými slovy, ze všech binomických koeficientů se dá vytknout pětka a 4+1=5.
Odtud se tvrdí, že dokazované tvrzení platí pro všechna přirozená čísla n.
Offline
#3 08. 05. 2009 16:27
- PitBull~--!
- Příspěvky: 208
- Reputace: 0
Re: injukce
↑ Marian:
mam tady jeste problem stimhle prikladem n^2 delitelny 3 a je to neprimy dukaz nebo dukaz sporem doufam ze sem to neopsal blbe.
potreboval bych vedet jak se to resi jako ten predchozi priklad
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#4 09. 05. 2009 12:54 — Editoval Marian (09. 05. 2009 12:55)
Re: injukce
↑ PitBull~--!:
Nelze dokazovat nepravidava tvzeni. Pokud platí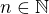 
, pak není npravda, že 
. Lehce se to nahlédne tak, že vemeš třeba číslo n=2. Pak jistě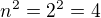 
není celočíselný násobek trojky. Spor! Odtud plyne, že dokazovat toto tvrzení (pokud si jej napsal správně a já jej správně pochopil) není nutné.
Offline