Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 03. 2017 16:21
Kvadraticka nerovnice a absolutni hodnotou
Dobry den,
mam priklad:
nulove body: 1, -1
Tabulka: (-∞;-1> <-1,1> <1,∞) nulové body do reseni patri, pze je v zadani  , je to tak?
, je to tak? - + -
- + -
I a III interval bude resen stejne:
-( )
) 
 (x+1)
(x+1)
2 -x-3
-x-3 0
0
resenim kvadraticke rovnice je -1 a 3/2
Otazka: musim udelat prunik <-1,3/2> - patri tam krajni body? Myslim, ze ano, v zadani je rovno nebo mensi s (-∞;-1> a <1,∞) - patri tam hodnoty -1 a 1? ja myslim, ze opet ano.
Prunik by tedy mel byt K1 =  <1;3/2> je to spravne?
<1;3/2> je to spravne?
II interval
( )
) 
 (x+1)
(x+1)
2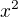 +x-1
+x-1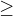 0
0
resenim kvadraticke rovnice je -1 a 1/2
Resenim je prunik intervalu <-1;1> a (-∞;-1> a <1/2,∞), tzn. K2 =  je to tak?
je to tak?
Otazka na tenhle priklad - patri do reseni i jednotlive nulove body? Je K1 a K2 spravne?
H
Offline
#2 01. 03. 2017 16:31
Re: Kvadraticka nerovnice a absolutni hodnotou
↑ Hanuna2:
Zdravím,
všechna řešení i rozhodnutí máš správně. Stačí jen určit konečný výsledek.
Offline
#4 01. 03. 2017 17:19
Re: Kvadraticka nerovnice a absolutni hodnotou
↑ Hanuna2:
Řešením není průnik, ale sjednocení množin. Zapsané to máš dobře, vyjádření je chybné.
průnik 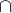 , sjednocení
, sjednocení 
Offline


 .
.